
分析 (1)先移项,再根据平方差公式因式分解,从而得到两个一元一次方程,解方程即可求解;
(2)先移项,再根据完全平方公式因式分解,从而得到一个一元一次方程,解方程即可求解.
解答 解:(1)(3x-2)2=4(x-3)2,
(3x-2)2-4(x-3)2=0,
(3x-2+2x-6)(3x-2-2x+6)=0,
(5x-8)(x+4)=0,
5x-8=0,x+4=0,
解得x1=1.6,x2=-4;
(2)(2x-1)2+4=4(2x-1),
(2x-1)2-4(2x-1)+4=0,
(2x-1-2)2=0,
2x-3=0,
解得x=1.5.
点评 考查了解一元二次方程-因式分解法,因式分解法解一元二次方程的一般步骤:
①移项,使方程的右边化为零;②将方程的左边分解为两个一次因式的乘积;③令每个因式分别为零,得到两个一元一次方程;④解这两个一元一次方程,它们的解就都是原方程的解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
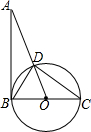 如图,AB=12,且AB为⊙O的切线,BC为⊙O的直径,AO与⊙O交于点D、AD=8.
如图,AB=12,且AB为⊙O的切线,BC为⊙O的直径,AO与⊙O交于点D、AD=8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 它是一个无理数 | |
| B. | 它是数轴上离原点$\sqrt{7}$个单位长度的点表示的数 | |
| C. | 若a<$\sqrt{7}$<a+1,则整数a为2 | |
| D. | 它表示面积为7的正方形的边长 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\sqrt{2}+\sqrt{5}$)$\sqrt{7}$=$\sqrt{7}$×$\sqrt{7}$=7 | B. | ($\sqrt{5}+\sqrt{3}$)($\sqrt{5}-\sqrt{2}$)=5-$\sqrt{6}$ | C. | ($\sqrt{3}-\sqrt{2}$)($\sqrt{3}+\sqrt{2}$)=3-2=1 | D. | ($\sqrt{5}-\sqrt{3}$)2=5-3=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+b)÷c | B. | a-b厘米 | C. | $1\frac{1}{3}x$ | D. | $\frac{4}{3}y$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com