
【题目】折纸与证明﹣﹣﹣用纸折出黄金分割点:
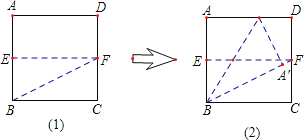
第一步:如图(1),先将一张正方形纸片ABCD对折,得到折痕EF;再折出矩形BCFE的对角线BF.
第二步:如图(2),将AB边折到BF上,得到折痕BG,试说明点G为线段AD的黄金分割点(AG>GD)
【答案】见解析
【解析】
连接GF,设正方形的边长为1,由折纸第一步,可知DF=![]() ,在Rt△BCF中,根据勾股定理得出BF=
,在Rt△BCF中,根据勾股定理得出BF=![]() ,则A′F=
,则A′F=![]() ﹣1.设AG=A'G=x,则GD=1﹣x,在Rt△A′GF和Rt△DGF中,根据勾股定理由GF不变得出A′F2+A′G2=DF2+DG2,列出关于x的方程,解方程求出x=
﹣1.设AG=A'G=x,则GD=1﹣x,在Rt△A′GF和Rt△DGF中,根据勾股定理由GF不变得出A′F2+A′G2=DF2+DG2,列出关于x的方程,解方程求出x=![]() ,即可说明点G是AD的黄金分割点.
,即可说明点G是AD的黄金分割点.
如图,连接GF,设正方形ABCD的边长为1,则DF=![]() .
.
在Rt△BCF中,BF=![]() =
=![]() ,
,
则A′F=BF﹣BA′=![]() ﹣1.
﹣1.
设AG=A′G=x,则GD=1﹣x,
在Rt△A′GF和Rt△DGF中,有A'F2+A'G2=DF2+DG2,
即![]() ,
,
解得x=![]() ,
,
即点G是AD的黄金分割点(AG>GD).


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中:①ac>0;②a+b+c<0;③4a﹣2b+c<0;④2a+b<0;⑤4ac﹣b2<4a;⑥a+b>0中,其中正确的个数为( )
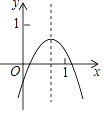
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出下列结论:①△DAG≌△DFG;②BG=2AG;③△EBF∽△DEG;④S△BEF=![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
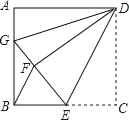
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
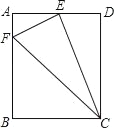
【题目】已知:如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F(AB>AE).问:△AEF与△EFC是否相似?若相似,证明你的结论;若不相似,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连结AD,下列说法:①∠BCE=∠ACD;②△ACD∽△BCE;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为![]() .其中正确的结论是_________.
.其中正确的结论是_________.
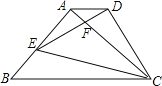
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的直角边BC在x轴负半轴上,斜边AC上的中线BD的反向延长线交y轴负半轴于点E,反比例函数y=﹣![]() (x<0)的图象过点A,则△BEC的面积是_____.
(x<0)的图象过点A,则△BEC的面积是_____.
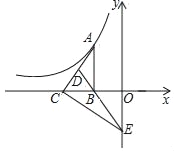
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,横坐标为a的点A在反比例函数y1=![]() (x>0)的图象上.点A与点A关于点O对称,一次函数y2=mx+n的图象经过点A.
(x>0)的图象上.点A与点A关于点O对称,一次函数y2=mx+n的图象经过点A.
(1)设a=2,点B(4,2)在函数y1,y2的图象上.
①分别求函数y1,y2的表达式;
②直接写出使y1>y2>0成立的x的范围.
(2)如图,设函数y1,y2的图象相交于点B,点B的横坐标为3a,△AA′B的面积为16,求k的值.
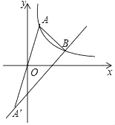
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB、AC上.

(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长;
(3)如果把它加工成矩形零件如图2,问这个矩形的最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行,通道水平宽度BC为8米,∠BCD=135°,通道斜面CD的长为6米,通道斜面AB的坡度i=1:![]() .
.
(1)求通道斜面AB的长;
(2)为增加市民行走的舒适度,拟将设计图中的通道斜面CD的坡度变缓,修改后的通道斜面DE的坡角为30°,求此时BE的长.
(答案均精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈2.24,
≈2.24,![]() ≈2.45)
≈2.45)
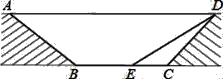
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com