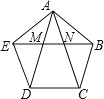
【题目】如图，在正五边形ABCDE中，对角线AD，AC与EB分别交于点M，N，则下列结论正确的是（ ）
A．EM：AE=2：(
-1)
B．MN：EM=(
-1)：(3-)
C．AM：MN=(3-)：(-1)
D．MN：DC=(3-)：2
【答案】D
【解析】
试题分析：根据正五边形的性质得到∠DAE=∠DAE，∠ADE=∠AEM=36°，推出△AME∽△AED，根据相似三角形的性质得到，得到AE2=ADAM，等量代换即可得到论．
∵五边形ABCDE是正五边形， ∴DE=AE=AB，∠AED=∠EAB=108°， ∴∠ADE=∠AEM=36°，
∴△AME∽△AED， ∴
， ∴AE2=ADAM， ∵AE=DE=DM， ∴DM2=ADAM，
设AE=DE=DM=2， ∴22=AM（AM+2）， ∴AM=
﹣1，（负值设去）， ∴EM=BN=AM=﹣1，AD=+1， ∵BE=AD， ∴MN=BE﹣ME﹣BN=3﹣， ∴MN：CD=(3-)：2
科目：初中数学 来源： 题型：
【题目】已知二次函数y=ax2+bx+c（a≠0），其中自变量x与函数值y之间满足下面的对应关系：
x | …… | 3 | 5 | 7 | …… |
y | …… | 3.5 | 3.5 | -2 | …… |
则a+b+c=______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】综合题。
（1）计算：﹣12016+（﹣5）×[（﹣2）3+2]﹣（﹣4）2÷（﹣ 
）
（2）解方程：x﹣ 
=2﹣ 
（3）已知：A= a﹣2（a﹣ 
b2），B=﹣ 
a+ 
b2 ， 且|a+2|+（b﹣3）2=0，求2A﹣6B的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】1号探测气球从海拔5 m处出发，以l m/min的速度上升．与此同时，2号探测气球从海拔15 m处出发，以0.5 m/min的速度上升，两个气球都匀速上升了50 min.设气球上升的时间为x(min)(0≤x≤50)．
(1)根据题意，填写下表：
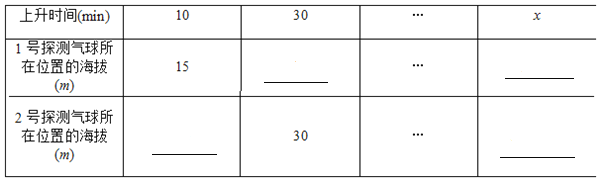
(2)在某时刻两个气球能否位于同一高度？如果能，这时气球上升了多长时间？位于什么高度？如果不能，请说明理由．
(3)当30≤x≤50时，两个气球所在位置的海拔最多相差多少米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如果2m9﹣xny和﹣3m2yn3x+1是同类项，则2m9﹣xny+（﹣3m2yn3x+1）=（ ）
A.﹣m8n4
B.mn4
C.﹣m9n
D.5m3n2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com