
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
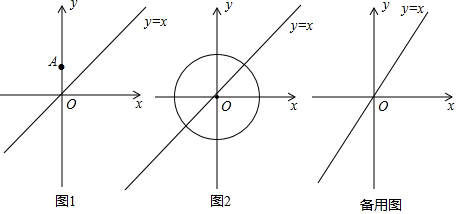
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
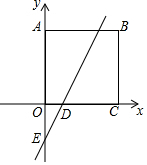 如图,矩形ABCD的顶点B坐标为(5,4),直线y=2x-3分别交x轴、y轴于D、E点,若线段BC上有一点P,直线DE上有一点Q,△APQ是以AP为斜边的等腰直角三角形,则点P坐标为(5,1)或(5,3).
如图,矩形ABCD的顶点B坐标为(5,4),直线y=2x-3分别交x轴、y轴于D、E点,若线段BC上有一点P,直线DE上有一点Q,△APQ是以AP为斜边的等腰直角三角形,则点P坐标为(5,1)或(5,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某商家为了给新产品作宜传,向全社会征集广告用语及商标图案,结果如图所示的商标(图中阴影部分)中标,求此商标图案的面积.(虚线左边为扇形,右边为长方形)
某商家为了给新产品作宜传,向全社会征集广告用语及商标图案,结果如图所示的商标(图中阴影部分)中标,求此商标图案的面积.(虚线左边为扇形,右边为长方形)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
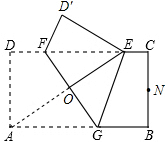 如图,矩形纸片ABCD中,AD=1,AB=2.将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB、CD交于点G、F,AE与FG交于点O.当△AED的外接圆与BC相切于BC的中点N.则折痕FG的长为$\frac{17}{15}$.
如图,矩形纸片ABCD中,AD=1,AB=2.将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB、CD交于点G、F,AE与FG交于点O.当△AED的外接圆与BC相切于BC的中点N.则折痕FG的长为$\frac{17}{15}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
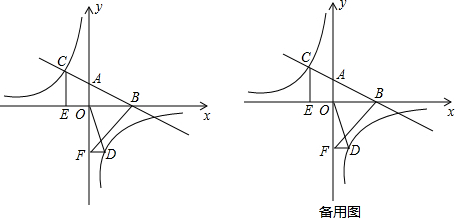
 如图,已知AB为⊙O直径,过⊙O上一点C作⊙O的切线,交AB延长线于点E,作AD⊥CE,交EC延长线于D,交⊙O于点F,设∠ABC=α(0°<α<90°).
如图,已知AB为⊙O直径,过⊙O上一点C作⊙O的切线,交AB延长线于点E,作AD⊥CE,交EC延长线于D,交⊙O于点F,设∠ABC=α(0°<α<90°).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com