
【题目】定义:在平面直角坐标系中,某个函数图象上任意两点的坐标分别为(x1,y1),(x2,y2),且x1≤x2,d=|y1-y2|.将这个函数图象在直线y=y1下方部分沿直线y=y1翻折,并将其向上平移d个单位,将这部分图象与原函数图象剩余部分的图象组成的新图象记为G,图象G对应的函数叫做这个函数的伴随函数.例如:点A(1,0)、B(2,1)在一次函数y=x-1的图象上,则它的伴随函数为![]() .
.
(1)点A、B在直线y=-2x上,点A在第二象限,点B在x轴上.当d=2时,求函数y=-2x的伴随函数所对应的函数表达式.
(2)二次函数y=x2-2x-3的图象交x轴负半轴交于点A,点B在抛物线上,设点B的横坐标为m.
①当d=0时,求该抛物线的伴随函数的图象G与直线y=4在第一象限的交点坐标;
②若直线y=2与该抛物线的伴随函数的图象G有四个交点,直接写出m的取值范围.
(3)抛物线y=x2-2nx+n2-n-1与y轴交于点A,点B在点A的左侧抛物线上,且d=1,当该抛物线的伴随函数的图象G上的点到x轴距离的最小值为1时,直接写出n的值.
【答案】(1)![]() ;(2)①图象G与直线y=4在第一象限的交点坐标为
;(2)①图象G与直线y=4在第一象限的交点坐标为![]() 或(1,4);②
或(1,4);②![]() 或
或![]() ;(3)n的值为-1或2.
;(3)n的值为-1或2.
【解析】
(1)点B在x轴上,故点B(0,0),d=2,则点A的纵坐标为2,求出点A的坐标,进而求解;
(2)①d=0,则m2﹣2m﹣3=0,则m=﹣1或m=3,故B(3,0),即可求解;②d=|m2﹣2m﹣3|<2,即可求解;
(3)①当点A在y轴下方时,翻折前的函数与x轴有交点,故图象G上的点到x轴距离的最小值为0,不合题意;②当点A在y轴上方时,图象G的最低点为点A,即n2﹣n﹣1=1,即可求解.
解:(1)∵点B在x轴上,
故点B(0,0),
∵d=2,则点A的纵坐标为2,
故2=-2x,
解得:x=-1,
故A(-1,2),
设翻折后的函数表达式为:y=2x+b,
将点A的坐标代入上式得:2=-2+b,
解得:b=4,
故翻折部分平移后函数的表达式为:y=2x+4+d=2x+6,
故伴随函数的表达式为:![]() ;
;
(2)y=x2-2x-3,令y=0,则x=-1或3,
故点A的坐标为:(-1,0),
设:B(m,m2-2m-3),
①d=0,则m2-2m-3=0,
∴m=-1或m=3,
∴B(3,0),
∴伴随函数为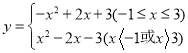 ;
;
当x<-1或x>3,y=4=x2-2x-3,
解得:![]() (舍去负值);
(舍去负值);
当-1≤x≤3时,y=4=-x2+2x+3,
解得:x=1;
∴图象G与直线y=4在第一象限的交点坐标为:![]() 或(1,4);
或(1,4);
②d=|m2-2m-3|<2,
∴-2<m2-2m-3<2,
∴![]() 或
或![]() ;
;
(3)y=x2-2nx+n2-n-1,
令x=0,则y=n2-n-1,
故点A(0,n2-n-1);
①当点A在y轴下方时,
翻折前的函数与x轴有交点,
故图象G上的点到x轴距离的最小值为0,不合题意;
②当点A在y轴上方时,
图象G的最低点为点A,即n2-n-1=1,
解得:n=-1或2,
故n的值为-1或2.


科目:初中数学 来源: 题型:
【题目】居民人均可支配收入、居民人均消费总支出和恩格尔系数都是反映居民生活水平的指标,其中恩格尔系数指居民家庭中食品支出占消费总支出的比重,恩格尔系数越小,说明食品支出占消费总支出比重越低,居民家庭越富裕,反之越贫穷.
下面是根据从权威机构获得的部分数据绘制的统计图:
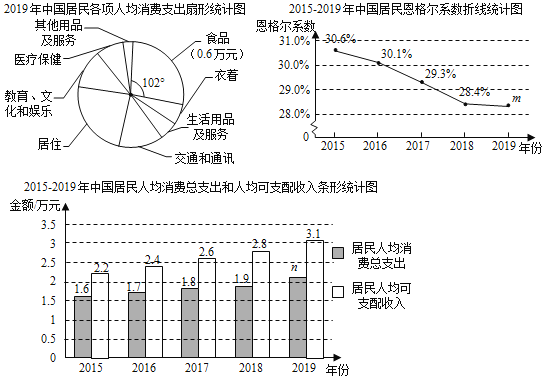
根据以上信息,回答下列问题:
(1)2019年中国城乡居民恩格尔系数m约为 (精确到0.1%);
(2)2019年居民人均消费总支出n约为 万元(精确到千位);
(3)下面的推断合理的是 .
①2015﹣2019年中国城乡居民人均可支配收入和人均消费总支出均呈逐年上升的趋势,说明中国居民生活水平逐步提高;
②2015﹣2019年中国城乡居民恩格尔系数呈现下降趋势,说明中国居民家庭富裕程度越来越高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宏兴企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系: ![]() .
.
(1)工人甲第几天生产的产品数量为70件?
(2)设第x天生产的产品成本为P元/件,P与x的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时,利润最大,最大利润是多少?
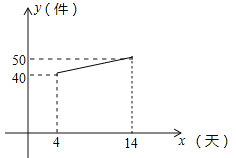
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△PQN中,若∠P=![]() ∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.
∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.
(1)已知△ABC是等边三角形,判断△ABC是否为“差角三角形”,并说明理由;
(2)在△ABC中,∠C=90°,50°≤∠B≤70°,判断△ABC是否为“差角三角形”,若是,请写出所有的“差角”并说明理由;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校七年级学生每周上网的时间,甲、乙两名学生进行了抽样调查.甲同学调查了七年级电脑爱好者中40名学生每周上网的时间;乙同学从全校800名七年级学生中随机抽取了40名学生,调查了每周上网的时间.甲、乙同学各自整理的样本数据如表:
上网时间t(小时/周) | 甲学生抽样人数(人) | 乙学生抽样人数(人) |
0≤t<1.5 | 6 | 22 |
1.5≤t<2.5 | 10 | 10 |
2.5≤t<3.5 | 16 | 6 |
t≥3.5 | 8 | 2 |
(1)你认为哪名学生抽取的样本不合理,请说明理由.
(2)请你根据抽取样本合理的学生的数据,将调查结果绘制成合适的统计图(绘制一种即可).
(3)专家建议每周上网2.5小时以上(含2.5小时)的学生应适当减少上网的时间,估计该校全体七年级学生中应适当减少上网的时间的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗击新冠肺炎疫情期间,市场上防护口罩出现热销.某药店用![]() 元购进甲,乙两种不同型号的口罩共
元购进甲,乙两种不同型号的口罩共![]() 个进行销售,已知购进甲种口罩与乙种口罩的费用相同,购进甲种口罩单价是乙种口罩单价的
个进行销售,已知购进甲种口罩与乙种口罩的费用相同,购进甲种口罩单价是乙种口罩单价的![]() 倍.
倍.
![]() 求购进的甲,乙两种口罩的单价各是多少?
求购进的甲,乙两种口罩的单价各是多少?
![]() 若甲,乙两种口罩的进价不变,该药店计划用不超过
若甲,乙两种口罩的进价不变,该药店计划用不超过![]() 元的资金再次购进甲,乙两种口罩共
元的资金再次购进甲,乙两种口罩共![]() 个,求甲种口罩最多能购进多少个?
个,求甲种口罩最多能购进多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】松山区种子培育基地用A,B,C三种型号的甜玉米种子共1500粒进行发芽试验,从中选出发芽率高的种子进行推广,通过试验知道,C型号种子的发芽率为80%,根据试验数据绘制了下面两个不完整的统计图:
(1)求C型号种子的发芽数;
(2)通过计算说明,应选哪种型号的种子进行推广?
(3)如果将所有已发芽的种子放在一起,从中随机取出一粒,求取到C型号发芽种子的概率.
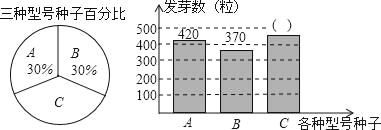
查看答案和解析>>
科目:初中数学 来源: 题型:
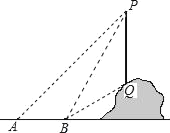
【题目】 如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走9m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.在Rt△ABC中,∠ACB=90°,AC=6,BC=8.点D是BC边上一点,连接AD,若△ABD是准互余三角形,则BD的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com