
【题目】抛物线y=ax2+bx+c(a≠0)图象的一部分如图所示,其对称轴为x=2,与x轴的一个交点是(﹣1,0),有以下结论:①abc>0;②4a﹣2b+c<0;③4a+b=0④抛物线与x轴的另一个交点是(5,0)⑤若点(﹣3,y1)(﹣6,y2)都在抛物线上,则y1<y2.其中正确的是_____.(只填序号)
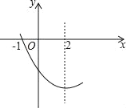
【答案】①③④⑤
【解析】
①先确定a、b、c的符号,再确定abc的符号;②根据当x=-2时,y的符号来确定4a-2b+c的符号;③根据对称轴:x=-![]() =2,化简得出;④由对称性得出结论;⑤利用增减性得出y1和y2的大小.
=2,化简得出;④由对称性得出结论;⑤利用增减性得出y1和y2的大小.
解:①∵抛物线开口向下,
∴a<0,
∵对称轴是:x=2,
∴a、b异号,
∴b>0,
∵抛物线与y轴交于负半轴,
∴c<0,
∴abc>0,
∴选项①正确;
②由图象得:当x=-2时,y>0,
∴4a-2b+c>0,
∴选项②不正确;
③抛物线对称轴是:x=-![]() =2,b=-4a,4a+b=0,
=2,b=-4a,4a+b=0,
∴选项③正确;
④由对称性得:抛物线与x轴的另一个交点为(5,0),
∴选项④正确;
⑤∵对称轴是:x=2,且开口向上,
∴当x<2时,y随x的增大而减小,
∵-3>-6,
∴y1<y2,
∴选项⑤正确;
故答案为:①③④⑤.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
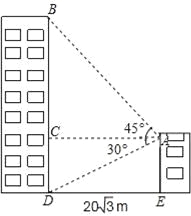
【题目】小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为20![]() 米.
米.
(1)求出大厦的高度BD;
(2)求出小敏家的高度AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形 ![]() 是菱形,
是菱形,![]() B=6,且∠ABC=60° ,M是菱形内任一点,连接AM,BM,CM,则AM+BM+CM 的最小值为________。
B=6,且∠ABC=60° ,M是菱形内任一点,连接AM,BM,CM,则AM+BM+CM 的最小值为________。

查看答案和解析>>
科目:初中数学 来源: 题型:
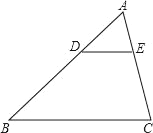
【题目】如图,已知△ABC∽△ADE,AB=30cm,BD=18cm,BC=20cm,∠BAC=75°,∠ABC=40°.
求:(1)∠ADE和∠AED的度数;
(2)DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=![]() DQ,求点F的坐标.
DQ,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:
![]()

(1)猜测y与x之间的函数关系,求出函数关系式并加以验证;
(2)当砝码的质量为24 g时,活动托盘B与点O的距离是多少?
(3)将活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在宣传“民族团结”活动中,采用四种宣传形式:A.器乐,B.舞蹈,C.朗诵,D.唱歌.每名学生从中选择并且只能选择一种最喜欢的,学校就宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.
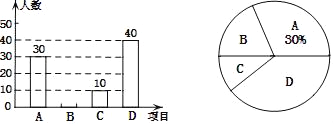
请结合图中所给信息,解答下列问题:
(1)本次调查的学生共有_____人;
(2)补全条形统计图;
(3)该校共有1200名学生,请估计选择“唱歌”的学生有多少人?
(4)七年一班在最喜欢“器乐”的学生中,有甲、乙、丙、丁四位同学表现优秀,现从这四位同学中随机选出两名同学参加学校的器乐队,请用列表或画树状图法求被选取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
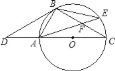
【题目】如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且∠DBA=∠BCD.
(1)根据你的判断:BD是⊙O的切线吗?为什么?.
(2)若点E是劣弧BC上一点,AE与BC相交于点F,且△BEF的面积为10,cos∠BFA=![]() ,那么,你能求出△ACF的面积吗?若能,请你求出其面积;若不能,请说明理由.
,那么,你能求出△ACF的面积吗?若能,请你求出其面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
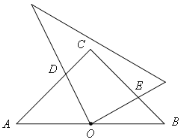
【题目】如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=![]() cm,将一块直角三角板的直角顶点放在点O处旋转,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE=______cm.
cm,将一块直角三角板的直角顶点放在点O处旋转,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE=______cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com