
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.

(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O以每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则 t的值为 秒(直接写出结果).
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,试探索:在旋转过程中,∠AOM与∠NOC的差是否发生变化?若不变,请求出这个差值;若变化,请求出差的变化范围.
【答案】(1)直线ON平分∠AOC;(2)12或30秒;(3)差为定值30°.
【解析】试题分析:(1)直线ON平分∠AOC,设ON的反向延长线为OD,已知OM平分∠BOC,根据角平分线的定义可得∠MOC=∠MOB,又由OM⊥ON,根据垂直的定义可得∠MOD=∠MON=90°,所以∠COD=∠BON,再根据对顶角相等可得∠AOD=∠BON,即可∴∠COD=∠AOD,结论得证;(1)已知∠BOC=120°,根据平角的定义可得∠AOC=60°,旋转至直线ON恰好平分锐角∠AOC,可得旋转120°或300°时ON平分∠AOC,由此可得10t=120°或300°,所以n=12或30;(3)差为定值30°,因为∠MON=90°,∠AOC=60°,所以∠AOM=90°-∠AON,∠NOC=60°-∠AON,再根据角的的和差计算即可.
试题解析:
(1)直线ON平分∠AOC.理由:
设ON的反向延长线为OD,
∵OM平分∠BOC,
∴∠MOC=∠MOB,
又∵OM⊥ON,
∴∠MOD=∠MON=90°,
∴∠COD=∠BON,
又∵∠AOD=∠BON(对顶角相等),
∴∠COD=∠AOD,
∴OD平分∠AOC,即直线ON平分∠AOC.
(2)12或30秒
(3)差为定值30°
∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°-∠AON、∠NOC=60°-∠AON,
∴∠AOM-∠NOC=(90°-∠AON)-(60°-∠AON)=30°.


科目:初中数学 来源: 题型:
【题目】根据题意解答
(1)已知x= ![]() +1,y=
+1,y= ![]() ﹣1,求下列各式的值. ①x2+2xy+y2
﹣1,求下列各式的值. ①x2+2xy+y2
②x2﹣y2
(2)先化简,再求值: ![]() ÷(
÷( ![]() ﹣a),其中a=
﹣a),其中a= ![]() ﹣2.
﹣2.
查看答案和解析>>
科目:初中数学 来源: 题型:
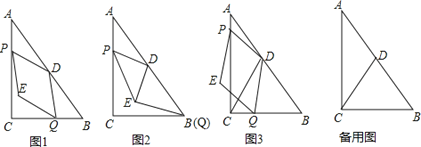
【题目】如图1,Rt△ABC中,∠ACB=Rt∠,AC=8,BC=6,点D为AB的中点,动点P从点A出发,沿AC方向以每秒1个单位的速度向终点C运动,同时动点Q从点C出发,以每秒2个单位的速度先沿CB方向运动到点B,再沿BA方向向终点A运动,以DP,DQ为邻边构造PEQD,设点P运动的时间为t秒.
(1)当t=2时,求PD的长;
(2)如图2,当点Q运动至点B时,连结DE,求证:DE∥AP.
(3)如图3,连结CD.
①当点E恰好落在△ACD的边上时,求所有满足要求的t值;
②记运动过程中PEQD的面积为S,PEQD与△ACD的重叠部分面积为S1,当![]() <
<![]() 时,请直接写出t的取值范围是 ______ .
时,请直接写出t的取值范围是 ______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)若∠AOC=50°,求出∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
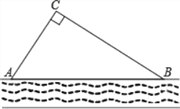
【题目】某校生物兴趣小组把一块沿河的三角形废地(如图)开辟为生物园(设AB段河岸为直线),已知∠ACB=90°,∠CAB=55°,BC=80米,学校决定在点C处建一个蓄水池,利用管道从河中取水,已知每铺设1米管道费用为50元,求铺设管道的最低费用(精确到1元).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A校和B校分别库存有电脑12台和6台,现决定支援给C校10台和D校8台.已知从A校调运一台电脑到C校和D校的运费分别为40元和10元;从B校调运一台电脑到C校和D校的运费分别为30元和20元. 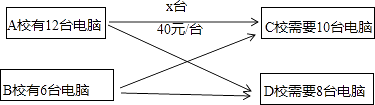
(1)设A校运往C校的电脑为x台,请仿照下图,求总运费W(元)关于x的函数关系式;
(2)求出总运费最低的调运方案,最低运费是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com