
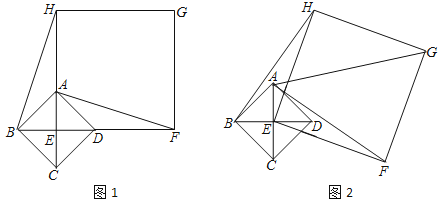
【题目】如图1,已知四边形ABCD是正方形,对角线AC、BD相交于点E,以点E为顶点作正方形EFGH.
(1)如图1,点A、D分别在EH和EF上,连接BH、AF,BH和AF有何数量关系,并说明理由;
(2)将正方形EFGH绕点E顺时针方向旋转,如图2,判断BH和AF的数量关系,并说明理由.
【答案】(1)BH=AF,见解析;(2)BH=AF,见解析.
【解析】
(1)根据正方形的性质可得AE=BE,∠BEH=∠AEF=90°,然后利用“边角边”证明△BEH和△AEF全等,根据全等三角形对应边相等即可得证;
(2)根据正方形的性质得到AE=BE,∠BEA=90°,EF=EH,∠HEF=90°,然后利用“边角边”证明△BEH和△AEF全等,根据全等三角形的性质即可得到结论.
(1)BH=AF,理由如下:
在正方形ABCD中,AE=BE,∠BEH=∠AEF=90°,
∵四边形EFGH是正方形,
∴EF=EH,
在△BEH和△AEF中,
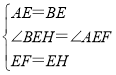 ,
,
∴△BEH≌△AEF(SAS),
∴BH=AF;
(2)BH=AF,理由如下:
∵四边形ABCD是正方形,
∴AE=BE,∠BEA=90°,
∵四边形EFGH是正方形,
∴EF=EH,∠HEF=90°,
∴∠BEA+∠AEH=∠HEF+∠AEH,
即∠BEH=∠AEF,
在△BEH与△AEF中,
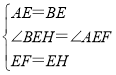 ,
,
∴△BEH≌△AEF(SAS),
∴BH=AF.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某市“艺术节”期间,小明、小亮都想去观看茶艺表演,但是只有一张茶艺表演 门票,他们决定采用抽卡片的办法确定谁去.规则如下:
将正面分别标有数字 1、2、3、4 的四张卡片(除数字外其余都相同)洗匀后,背面朝上 放置在桌面上,随机抽出一张记下数字后放回;重新洗匀后背面朝上放置在桌面上, 再随机抽出一张记下数字.如果两个数字之和为奇数,则小明去;如果两个数字之和 为偶数,则小亮去.
(1)请用列表或画树状图的方法表示抽出的两张卡片上的数字之和的所有可能出现 的结果;
(2)你认为这个规则公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设 A 是由 2×4 个整数组成的 2 行 4 列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.数表A 如下表所示,如果经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负整数,请写出每次“操作”后所得的数表.(写出一种方法即可)
1 | 2 | 3 | -7 |
-2 | -1 | 0 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】预计用1500元购买甲商品x个,乙商品y个,不料甲商品每个涨价1.5元,乙商品每个涨价1元,尽管购买甲商品的个数比预定数减少10个,总金额仍多用29元.又若甲商品每个只涨价1元,并且购买甲商品的数量只比预定数少5个, 乙商品仍每个涨价1元,那么甲、乙两商品支付的总金额是1563.5元.
(1)求x、y的关系式;
(2)若预计购买甲商品的个数的2倍与预计购买乙商品的个数的和大于205,但小于210,求x,y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
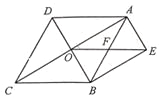
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若OE=10,AC=16,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解全校学生上学的交通方式,我校九年级(21)班的5名同学联合设计了一份调查问卷,对该校部分学生进行了随机调查.按A(骑自行车)、B(乘公交车)、C(步行)、D(乘私家车)、E(其他方式)设置选项,要求被调查同学从中单选.并将调查结果绘制成条形统计图1和扇形统计图2,根据以上信息,解答下列问题:
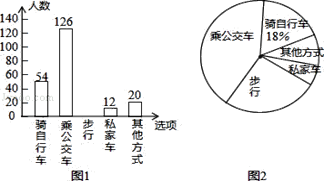
(1)本次接受调查的总人数是 人,其中“步行”的人数是 人;
(2)在扇形统计图中,“乘公交车”的人数所占的百分比是 ,“其他方式”所在扇形的圆心角度数是 ;
(3)已知这5名同学中有2名女同学,要从中选两名同学汇报调查结果.请你用列表法或画树状图的方法,求出恰好选出1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
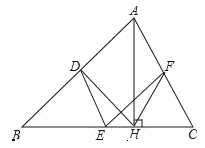
【题目】如图,在△ABC中,点D、E、F分别是边AB、BC、CA的中点,AH是边BC上的高.
(1)求证:四边形ADEF是平行四边形;
(2)若∠AHF=20°,∠AHD=50°,求∠DEF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com