
【题目】如图是某月的日历表,在此目历表上可以用一个“十”字圈出5个数.
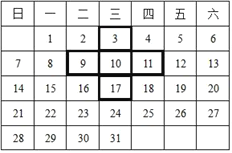
(1)如图中四周的4个数3、9、17、11的和与中间的数10有什么数量关系?
(2)照此方法,任意圈出的5个数是否都具有这样的数量关系?请通过整式的运算说明理由.
(3)用(2)的结论说明圈出的5个数的和能否等于125?
【答案】(1)数3、9、17、11的和与中间的数10是4倍关系;(2)任意圈出的5个数都具有这样的数量关系;(3)圈出的5个数的和不能等于125.
【解析】
(1)计算出四周的4个数的和,与中间的数进行比较即可;(2)设第二行中间数为x,则其他四个数分别为x﹣7,x﹣1,x+1,x+7,计算这四个数的和为4x,是4的倍数,即可得任意圈出的5个数都具有这样的数量关系;(3)根据(2)的方法可列出方程,求出x的值,再根据日历的天数判断即可.
(1)∵3+9+11+17=40,
40÷10=4,
∴数3、9、17、11的和与中间的数10是4倍关系;
(2)任意圈出的5个数都具有这样的数量关系,
设第二行中间数为x,则其他四个数分别为x﹣7,x﹣1,x+1,x+7,
∴x﹣7+x﹣1+x+1+x+7=4x,
∴任意圈出的5个数都具有这样的数量关系;
(3)x+4x=5x=125,
∴x=25,
∵25为中间数,
∴最大数为25+7=32,
∵日历没有32日,
∴圈出的5个数的和不能等于125.


科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.
(1)求∠CAM的度数;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
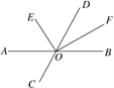
【题目】如图,直线AB、CD交于点O,OE平分∠AOD,OF平分∠BOD.
(1)∠AOC=50°,求∠DOF与∠DOE的度数,并计算∠EOF的度数;
(2)当∠AOC的度数变化时,∠EOF的度数是否变化?若不变,求其值;若变化,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋中有除颜色外其他完全相同的3个球,每次从袋中摸出一个球,记下颜色后放回搅匀再摸,在摸球试验中得到下表中部分数据:
摸球 总次数 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
摸到黄球的次数 | 14 | 23 | 38 | 52 | 67 | 86 | 97 | 111 | 120 | 136 |
摸到黄球的频率 | 35% | 32% | 33% | 35% | 35% |
(1)请将上表补充完整(结果精确到1%);
(2)制作折线统计图表示摸到黄球的频率的变化情况;
(3)估计从袋中摸出一个球是黄球的概率是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.
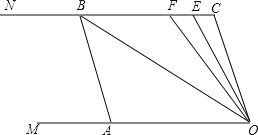
(1)请在图中找出与∠AOC相等的角,并说明理由;
(2)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=2∠OBA?若存在,请求出∠OBA度数;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2mx+m2+m+1的图象与x轴交于A、B两点,点C为顶点.
(1)求m的取值范围;
(2)若将二次函数的图象关于x轴翻折,所得图象的顶点为D,若CD=8.求四边形ACBD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD.
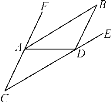
(1)判断∠FAB与∠C的大小关系,请说明理由;
(2)若∠C=35°,AB是∠FAD的平分线.
①求∠FAD的度数;
②若∠ADB=110°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
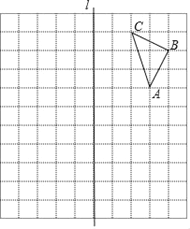
【题目】如图,直线l与△ABC在边长为1个单位长度的小正方形网格中,点A,B,C都为网格线的交点.
(1)请画出△ABC关于直线l对称的△A1B1C1(点A,B,C的对称点分别为A1,B1,C1).
(2)请画出将线段AC向左平移3个单位,再向下平移5个单位得到的线段A2C2(点A,C的对应点分别为A2,C2),再以A2C2为斜边画一个等腰直角三角形A2B2C2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com