
分析 根据已知条件判断a、b、c的符号两负一正,以及当a>0时,$\frac{a}{|a|}$=1,当a<0时,$\frac{a}{|a|}$=-1,可求x的值,将y的不等式变形为$\frac{b+c}{a}$+$\frac{a+c}{b}$+$\frac{a+b}{c}$,由a+b+c=0,得b+c=-a,a+c=-b,a+b=-c,可求y的值,代入所求算式即可
解答 解:由a+b+c=0,且abc>0,可知a、b、c三数中,两负一正,
∵当a>0时,$\frac{a}{|a|}$=1,当a<0时,$\frac{a}{|a|}$=-1,
∴x=$\frac{a}{|a|}$+$\frac{b}{|b|}$+$\frac{c}{|c|}$=-1,y=a($\frac{1}{b}$+$\frac{1}{c}$)+b($\frac{1}{a}$+$\frac{1}{c}$)+c($\frac{1}{a}$+$\frac{1}{b}$)=$\frac{b+c}{a}$+$\frac{a+c}{b}$+$\frac{a+b}{c}$=-3,
∴x2014-xy+y3=(-1)2014-(-1)×(-3)+(-3)3
=1-3-27=-29.
点评 本题考查了代数式的求值,运用了$\frac{a}{|a|}$=±1,同分母的运算,分类讨论的方法.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:解答题
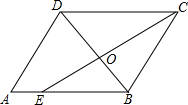 如图,在平行四边形ABCD中,CE是∠DCB的角平分线,且交AB于点E,DB与CE相交于点O,
如图,在平行四边形ABCD中,CE是∠DCB的角平分线,且交AB于点E,DB与CE相交于点O,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
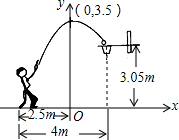 宜昌四中男子篮球队在2016全区篮球比赛中蝉联冠军,让全校师生倍受鼓舞.在一次与第25中学的比赛中,运动员小涛在距篮下4米处跳起投篮,如图所示,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
宜昌四中男子篮球队在2016全区篮球比赛中蝉联冠军,让全校师生倍受鼓舞.在一次与第25中学的比赛中,运动员小涛在距篮下4米处跳起投篮,如图所示,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10,24,26 | B. | 15,20,25 | C. | 8,10,12 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
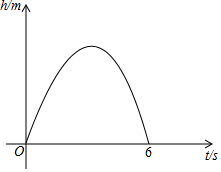 从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2(0≤t≤6).
从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2(0≤t≤6).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com