
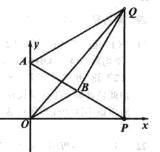
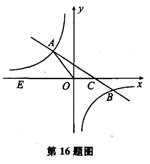
.如图,在平面直角坐标系中,已知点A(0,2),点P是x轴上一动点,以线段AP为一边,在其一侧作等边三角线APQ。当点P运动到原点O处时,记Q得位置为B。
(1)求点B的坐标;
(2)求证:当点P在x轴上运动(P不与Q重合)时,∠ABQ为定值;
(3)是否存在点P,使得以A、O、Q、B为顶点的四边形是梯形?若存在,请求出P点的坐标;若不存在,请说明理由。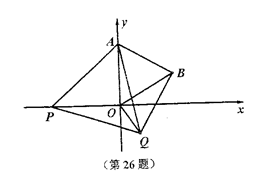
(1)过点B作BC⊥y轴于点C,∵A(0,2),△AOB为等边三角形,
∴AB=OB=2,∠BAO=60°,
∴BC=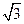 ,OC=AC=1,
,OC=AC=1,
即B(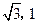 )
)
(2)当点P在x轴上运动(P不与O重合)时,不失一般性,
∵∠PAQ==∠OAB=60°,
∴∠PAO=∠QAB,
在△APO和△AQB中,
∵AP=AQ,∠PAO=∠QAB,AO=AB
∴△APO≌△AQB总成立,
∴∠ABQ=∠AOP=90°总成立,
∴当点P在x轴上运动(P不与Q重合)时,∠ABQ为定值90°。
(3)由(2)可知,点Q总在过点B且与AB垂直的直线上,
可见AO与BQ不平行。
① 当点P在x轴负半轴上时,点Q在点B的下方,
此时,若AB∥OQ,四边形AOQB即是梯形,
当AB∥OQ时,∠BQO=90°,∠BOQ=∠ABO=60°。
又OB=OA=2,可求得BQ=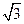 ,
,
由(2)可知,△APO≌△AQB,∴OP=BQ=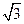 ,
,
∴此时P的坐标为( )。
)。
②当点P在x轴正半轴上时,点Q在嗲牛B的上方,
此时,若AQ∥OB,四边形AOQB即是梯形,
当AQ∥OB时,∠ABQ=90°,∠QAB=∠ABO=60°。
又AB= 2,可求得BQ=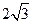 ,
,
由(2)可知,△APO≌△AQB,∴OP=BQ=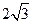 ,
,
∴此时P的坐标为( )。
)。
综上,P的坐标为( )或(
)或( )。
)。
解析


科目:初中数学 来源: 题型:
| 8 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
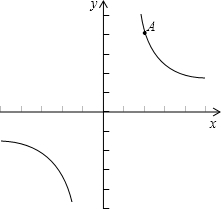
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=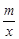 (m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=
(m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=![]() .
.
1.求该反比例函数和一次函数的解析式
2.求△AOC的面积
查看答案和解析>>
科目:初中数学 来源:2010年北京市丰台区中考数学二模试卷(解析版) 题型:解答题
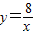 的图象经过点A.正比例函数y=kx的图象绕原点顺时针旋转90°后,恰好经过点A,求k的值.
的图象经过点A.正比例函数y=kx的图象绕原点顺时针旋转90°后,恰好经过点A,求k的值.
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(四川巴中卷)数学(解析版) 题型:解答题
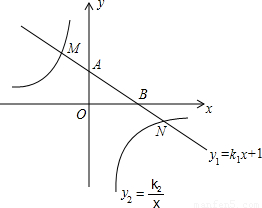
如图,在平面直角坐标系中,一次函数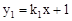 的图象与y轴交于点A,
的图象与y轴交于点A,
与x轴交于点B,与反比例函数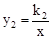 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
标为2,
(1)求一次函数和反比例函数的解析式;
(2)直接写出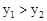 时x的取值范围。
时x的取值范围。
查看答案和解析>>
科目:初中数学 来源:2013届湖南省八年级反比例函数测试数学试卷(解析版) 题型:填空题
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=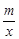 (m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=
(m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE= .
.
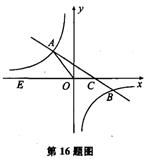
1.求该反比例函数和一次函数的解析式
2.求△AOC的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com