
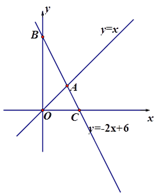
【题目】如图,直线![]() 与x轴、
与x轴、![]() 轴分别相交于点C、B,与直线
轴分别相交于点C、B,与直线![]() 相交于
相交于
点A.
(1)点B、点C和点A的坐标分别是(0, )、( ,0)、( , );
(2)求两条直线与![]() 轴围成的三角形的面积;
轴围成的三角形的面积;
(3)在坐标轴上是否存在一点Q,使△OAQ的面积等于6,若存在请直接写出Q点的坐标,若不存在,请说明理由.
【答案】(1) 6,3,2,2;(2)3;(3)存在,理由见解析.
【解析】分析:(1)根据坐标轴上点的坐标特征易得B点坐标为(0,6),C点坐标为(3,0),然后解方程组![]() 可确定A点坐标;(2)根据三角形面积公式计算;(3)分类讨论:当Q点在x轴上,设Q(a,0),则S△AOQ=
可确定A点坐标;(2)根据三角形面积公式计算;(3)分类讨论:当Q点在x轴上,设Q(a,0),则S△AOQ=![]() ×2×|a|=6;当Q点在y轴上,设Q(0,b),则S△AOQ=
×2×|a|=6;当Q点在y轴上,设Q(0,b),则S△AOQ=![]() ×2×|b|=6,然后分别求出a和b的值,从而得到Q点的坐标.
×2×|b|=6,然后分别求出a和b的值,从而得到Q点的坐标.
本题解析:
(1)把x=0代入y=2x+6得y=6,所以B点坐标为(0,6),
把y=0代入y=2x+6得2x+6=0,解得x=3,所以C点坐标为(3,0),
解方程组![]() 得
得![]() ,所以A点坐标为(2,2),
,所以A点坐标为(2,2),
故答案为6,3,2,2;
(2) ![]() =
=![]() ×3×2=3;
×3×2=3;
(3)存在。
当Q点在x轴上,设Q(a,0),则S△AOQ=![]() ×2×|a|=6,
×2×|a|=6,
解得a=±6,
则Q点坐标为(6,0)、(6,0);
当Q点在y轴上,设Q(0,b),则![]() =
=![]() ×2×|b|=6,
×2×|b|=6,
解得b=±6,
则Q点坐标为(0,6)、(0,6),
综上所述Q点坐标为(0,6)、(0,6)、(6,0)、(6,0).


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
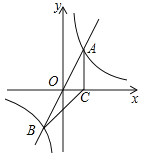
【题目】(2016四川省乐山市第24题)如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
(1)求k的值;
(2)x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂计划生产A、B两种产品共50件.已知A产品每件可获利润1200元,B产品每件可获利润700元,设生产两种产品的获利总额为y (元),生产A产品x (件).
(1)写出y与x之间的函数关系式;
(2)若生产A、B两种产品的件数均不少于10件,求总利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
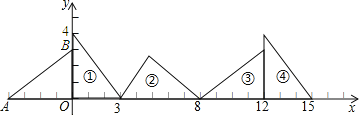
【题目】如图,在直角坐标系中,已知点A(-4,0),B(0,3),对△OAB连续作旋转变换,依
次得到三角形(1)、三角形(2)、三角形(3)、三角形(4)、…,
(1)△AOB的面积是_____________;
(2)三角形(2016)的直角顶点的坐标是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:
①该抛物线的对称轴在y轴左侧;
②关于x的方程ax2+bx+c+2=0无实数根;
③a﹣b+c≥0;
④![]() 的最小值为3.
的最小值为3.
其中,正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(-13)+(-18) (2)20+(-14)
(3)1.7 + 2.8 (4)2.3 + (-3.1)
(5)(-7![]() )+(-8) (6)1
)+(-8) (6)1![]() +(-1.5)
+(-1.5)
(7)(-3.04)+ 6 (8)8![]() +(-11)
+(-11)
(9)15+(-22) (10)(-13)+(-8)
(11)(-0.9)+1.5 (12) ![]() +(-
+(-![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com