
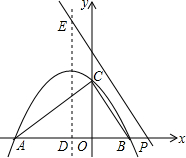
 如图,二次函数y=ax2+bx+3的图象抛物线与其对称轴交于点(-1,m),与x轴交于点A和点B(2,0),与y轴交于点C,其对称轴与x轴交于点D.
如图,二次函数y=ax2+bx+3的图象抛物线与其对称轴交于点(-1,m),与x轴交于点A和点B(2,0),与y轴交于点C,其对称轴与x轴交于点D.分析 (1)利用对称轴x=-1和B(2,0)列方程组求解即可;
(2)①求出直线BC的解析式y=$-\frac{3}{2}x+3$,因为PE∥BC,并且P(t+2,0),所以直线PE的解析式为:y=$-\frac{3}{2}x+\frac{3t}{2}+3$,然后用t表示出△PCE的面积,列方程求解;
②本问关键是理解“以A、B、M为顶点所作的直角三角形有且只有三个”的含义.因为过A、B点作x轴的垂线,其与直线l的两个交点均可以与A、B点构成直角三角形,这样已经有符合题意的两个直角三角形;第三个直角三角形从直线与圆的位置关系方面考虑,以AB为直径作圆,当直线与圆相切时,根据圆周角定理,切点与A、B点构成直角三角形.从而问题得解.注意:这样的切线有两条,如图2所示.
解答 解:(1)根据题意知,对称轴x=-1,图象过B(2,0) ,
,
∴$\left\{\begin{array}{l}{-\frac{b}{2a}=-1}\\{4a+2b+3=0}\end{array}\right.$,
解得:a=-$\frac{3}{8}$,b=-$\frac{3}{4}$,
∴二次函数的关系式为:y=$-\frac{3}{8}{x}^{2}-\frac{3}{4}x+3$;
(2)①如图1,
∵直线BC过B(2,0),C(0,3),
∴直线BC的解析式y=$-\frac{3}{2}x+3$,
∵PE∥BC,并且P(t+2,0),
∴直线PE的解析式为:y=$-\frac{3}{2}x+\frac{3t}{2}+3$,
∴E(-1,$\frac{3t+9}{2}$)
又∵D(-1,0),C(0,3),P(t+2,0),
∴OE=$\frac{3t+9}{2}$,PD=t+3,OC=3,OP=t+2,OD=1,OB=2,
∴S△PDE=$\frac{1}{2}•PD•DE$=$\frac{1}{2}•\frac{3t+9}{2}•(t+3)$=$\frac{3}{4}{t}^{2}+\frac{18}{4}t+\frac{27}{4}$,
S△OPC=$\frac{1}{2}•OP•OC$=$\frac{1}{2}×(t+2)×3$=$\frac{3t}{2}+3$,
S梯形OCDE=$\frac{1}{2}(OC+DE)•OD$=$\frac{3t+15}{4}$,
S△OBC=3,
∴S△PCE=S△PDE-S△OPC-S梯形OCDE=$\frac{3}{4}{t}^{2}+\frac{9}{4}t$,
当△PCE的面积为△OCB面积的7倍时,
$\frac{3}{4}{t}^{2}+\frac{9}{4}t$=3×7,
解得:t=4或t=-7(舍去)
∴当t为4时,△PCE的面积为△OCB面积的7倍;
②∵当以A、B、M为顶点所作的直角三角形有且只有三个时,第三个直角三角形以AB为直径作圆,当直线与圆相切时,根据圆周角定理,切点M与A、B点构成直角三角形,
∴当t=2时,P(4,0),以AB为直径作⊙D,圆心为D.过P点作⊙D的切线,这样的切线有2条.
如图2,连接DM,过M作MN⊥x轴于点N,
∵A(-4,0),B(2,0),
∴D(-1,0),⊙D半径DM=DB=3.
又∵DP=5,
∴在Rt△MPD中,
MP=$\sqrt{{5}^{2}-{3}^{2}}$=4,sin∠MDP=$\frac{4}{5}$,cos∠MDP=$\frac{3}{5}$.
在Rt△DMN中,MN=MD•sin∠MDP=3×$\frac{4}{5}$=$\frac{12}{5}$,
DN=MD•cos∠MDP=3×$\frac{3}{5}$=$\frac{9}{5}$,
则ON=DN-OD=$\frac{4}{5}$,
∴M点坐标为($\frac{4}{5}$,$\frac{12}{5}$)
直线l过M($\frac{4}{5}$,$\frac{12}{5}$),E(4,0),
设直线l的解析式为y=kx+b,则有
$\left\{\begin{array}{l}{\frac{4}{5}k+b=\frac{12}{5}}\\{4k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=3}\end{array}\right.$.
所以直线l的解析式为y=-$\frac{3}{4}$x+3.
同理,可以求得另一条切线的解析式为y=$\frac{3}{4}$x-3.
综上所述,直线l的解析式为y=-$\frac{3}{4}$x+3或y=$\frac{3}{4}$x-3.
点评 本题解题关键是二次函数、一次函数以及圆等知识的综合运用.难点在于第(3)问中对于“以A、B、M为顶点所作的直角三角形有且只有三个”条件的理解,这可以从直线与圆的位置关系方面入手解决.本题难度较大,需要同学们对所学知识融会贯通、灵活运用.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,二次函数的图象与x轴相交于点A(-3,0)、B(-1,0),与y轴相交于点C(0,3),点P是该图象上的动点;一次函数y=kx-4k(k≠0)的图象过点P交x轴于点Q.
如图,二次函数的图象与x轴相交于点A(-3,0)、B(-1,0),与y轴相交于点C(0,3),点P是该图象上的动点;一次函数y=kx-4k(k≠0)的图象过点P交x轴于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某校学生来自甲、乙、丙三个地区,其人数比为2:3:5,如图所示的扇形统计图表上述分布情况.已知来自甲地区的为160人,则下列说法不正确的是( )
某校学生来自甲、乙、丙三个地区,其人数比为2:3:5,如图所示的扇形统计图表上述分布情况.已知来自甲地区的为160人,则下列说法不正确的是( )| A. | 扇形甲的圆心角是72° | |
| B. | 学生的总人数是800人 | |
| C. | 丙地区的人数比乙地区的人数多160人 | |
| D. | 甲地区的人数比丙地区的人数少160人 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com