
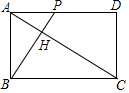
 »γΆΦΘ§“―÷ΣΨΊ–ΈABCD÷–Θ§AB=2Θ§AD=2$\sqrt{3}$Θ§Ε·ΒψP¥”ΒψA≥ωΖΔœρ÷’ΒψD‘ΥΕ·Θ§Ν§BPΘ§≤ΔΙΐΒψCΉςCHΓΆBPΘ§¥ΙΉψΈΣHΘ°ΔΌΒψH≤ΜΩ…Ρή‘ΎΨΊ–ΈABCD÷°ΆβΘΜΔΎAHΒΡΉν–Γ÷ΒΈΣ$\sqrt{7}$-$\sqrt{3}$ΘΜΔέ‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§BP…®ΙΐΒΡΟφΜΐ Φ÷’Β»”ΎCH…®ΙΐΒΡΟφΜΐΘΜΔή‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§ΒψHΒΡ‘ΥΕ·¬ΖœΏΘ®ΙλΦΘΘ©≥ΛΈΣ$\frac{2}{3}$$\sqrt{3}$Π–Θ§’ΐ»ΖΒΡ”–Θ®Χν–ρΚ≈Θ©ΔΌΔΎΔήΘ°
»γΆΦΘ§“―÷ΣΨΊ–ΈABCD÷–Θ§AB=2Θ§AD=2$\sqrt{3}$Θ§Ε·ΒψP¥”ΒψA≥ωΖΔœρ÷’ΒψD‘ΥΕ·Θ§Ν§BPΘ§≤ΔΙΐΒψCΉςCHΓΆBPΘ§¥ΙΉψΈΣHΘ°ΔΌΒψH≤ΜΩ…Ρή‘ΎΨΊ–ΈABCD÷°ΆβΘΜΔΎAHΒΡΉν–Γ÷ΒΈΣ$\sqrt{7}$-$\sqrt{3}$ΘΜΔέ‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§BP…®ΙΐΒΡΟφΜΐ Φ÷’Β»”ΎCH…®ΙΐΒΡΟφΜΐΘΜΔή‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§ΒψHΒΡ‘ΥΕ·¬ΖœΏΘ®ΙλΦΘΘ©≥ΛΈΣ$\frac{2}{3}$$\sqrt{3}$Π–Θ§’ΐ»ΖΒΡ”–Θ®Χν–ρΚ≈Θ©ΔΌΔΎΔήΘ° Ζ÷Έω ΗυΨίΒψHΒΡ‘ΥΕ·¬ΖœΏΘ®ΙλΦΘΘ©ΈΣ“‘OΈΣ‘≤–ΡΒΡ$\widehat{BQ}$Θ§Φ¥Ω…ΒΟ≥ωΒψH≤ΜΩ…Ρή‘ΎΨΊ–ΈABCD÷°ΆβΘΜΗυΨίΒ±AΘ§HΘ§O‘ΎΆ§“Μ÷±œΏ…œ ±Θ§AHΉνΕΧΘ§Φ¥Ω…ΒΟ≥ωAHΒΡΉν–Γ÷ΒΘΜΗυΨίBP…®ΙΐΒΡΟφΜΐ=ΓςABDΒΡΟφΜΐΘ§CH…®ΙΐΒΡΟφΜΐ=Β»±ΏΓςCOQΒΡΟφΜΐ+…»–ΈBOQΒΡΟφΜΐΘ§Φ¥Ω…ΒΟ≥ωBP…®ΙΐΒΡΟφΜΐ≤ΜΒ»”ΎCH…®ΙΐΒΡΟφΜΐΘΜΗυΨίΒψHΒΡ‘ΥΕ·¬ΖœΏΘ®ΙλΦΘΘ©ΈΣ$\widehat{BQ}$Θ§‘Υ”ΟΜΓ≥ΛΦΤΥψΙΪ ΫΦ¥Ω…ΒΟ≥ωΫαΙϊΘ°
Ϋβ¥π 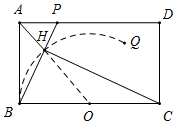 ΫβΘΚ»γΆΦΥυ ΨΘ§ΓΏCHΓΆBP”ΎHΘ§
ΫβΘΚ»γΆΦΥυ ΨΘ§ΓΏCHΓΆBP”ΎHΘ§
ΓύΓœBHC=90ΓψΘ§
ΓύΒψHΒΡ‘ΥΕ·¬ΖœΏΘ®ΙλΦΘΘ©ΈΣ“‘OΈΣ‘≤–ΡΒΡ$\widehat{BQ}$Θ§
ΓΏOH=OB=$\sqrt{3}$Θ§AB=2Θ§
ΓύOHΘΦABΘ§
ΓύΒψH≤ΜΩ…Ρή‘ΎΨΊ–ΈABCD÷°ΆβΘ§Ι ΔΌ’ΐ»ΖΘΜ
Ν§Ϋ”AHΘ§AOΘ§HOΘ§‘ρAH+HOΓίAOΘ§
ΓύΒ±AΘ§HΘ§O‘ΎΆ§“Μ÷±œΏ…œ ±Θ§AHΉνΕΧΘ§
¥Υ ±AH=AO-HO=$\sqrt{{2}^{2}+Θ®\sqrt{3}Θ©^{2}}$-$\sqrt{3}$Θ§
Φ¥AHΒΡΉν–Γ÷ΒΈΣ$\sqrt{7}$-$\sqrt{3}$Θ§Ι ΔΎ’ΐ»ΖΘΜ
Δέ»γΆΦΥυ ΨΘ§‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§BP…®ΙΐΒΡΟφΜΐ=ΓςABDΒΡΟφΜΐ=$\frac{1}{2}$ABΓΝAD=$\frac{1}{2}$ΓΝ2ΓΝ2$\sqrt{3}$=2$\sqrt{3}$Θ§
CH…®ΙΐΒΡΟφΜΐ=Β»±ΏΓςCOQΒΡΟφΜΐ+…»–ΈBOQΒΡΟφΜΐ=$\frac{\sqrt{3}}{4}$ΓΝΘ®$\sqrt{3}$Θ©2+$\frac{120ΓΝΠ–ΓΝΘ®\sqrt{3}Θ©^{2}}{360}$=$\frac{3}{4}\sqrt{3}$+Π–Θ§
ΓύBP…®ΙΐΒΡΟφΜΐ≤ΜΒ»”ΎCH…®ΙΐΒΡΟφΜΐΘ§Ι Δέ¥μΈσΘΜ
Δή‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§ΒψHΒΡ‘ΥΕ·¬ΖœΏΘ®ΙλΦΘΘ©≥ΛΈΣ$\widehat{BQ}$=$\frac{120ΓΝΠ–ΓΝ\sqrt{3}}{180}$=$\frac{2}{3}$$\sqrt{3}$Π–Θ§Ι Δή’ΐ»ΖΘΜ
Ι ¥πΑΗΈΣΘΚΔΌΔΎΔήΘ°
ΒψΤά ±ΨΧβ÷ς“ΣΩΦ≤ιΝΥΙλΦΘ“‘ΦΑΨΊ–ΈΒΡ–‘÷ ΒΡ‘Υ”ΟΘ§ΫβΧβ ±ΉΔ“βΘΚ÷±ΨΕΥυΕ‘ΒΡ‘≤÷ήΫ«ΈΣ÷±Ϋ«ΘΜΫβΨωΈ ΧβΒΡΙΊΦϋ «’ΤΈ’ΜΓ≥ΛΒΡΦΤΥψΙΪ Ϋ“‘ΦΑ…»–ΈΒΡΟφΜΐΦΤΥψΙΪ ΫΒΡ‘Υ”ΟΘ°


 Ή¥‘ΣΖΜ»Ϊ≥ΧΆΜΤΤΒΦΝΖ≤βœΒΝ–¥πΑΗ
Ή¥‘ΣΖΜ»Ϊ≥ΧΆΜΤΤΒΦΝΖ≤βœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 3x+2y=5Θ®x+yΘ© | BΘ° | x+x3=x4 | CΘ° | x2•x3=x6 | DΘ° | Θ®x2Θ©3=x6 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
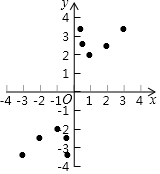 Ρ≥ΑύΓΑ ΐ―ß–Υ»Λ–ΓΉιΓ±Ε‘Κ· ΐy=x+$\frac{1}{x}$ΒΡΆΦœσΚΆ–‘÷ Ϋχ––ΝΥΧΫΨΩΘ§ΧΫΨΩΙΐ≥Χ»γœ¬Θ§«κ≤Ι≥δΆξ’ϊΘΚ
Ρ≥ΑύΓΑ ΐ―ß–Υ»Λ–ΓΉιΓ±Ε‘Κ· ΐy=x+$\frac{1}{x}$ΒΡΆΦœσΚΆ–‘÷ Ϋχ––ΝΥΧΫΨΩΘ§ΧΫΨΩΙΐ≥Χ»γœ¬Θ§«κ≤Ι≥δΆξ’ϊΘΚ| ΓΓx | Γ≠ | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | ΓΓ1 | ΓΓ2 | ΓΓ3 | Γ≠ |
| ΓΓy | Γ≠ | -$\frac{10}{3}$ | -$\frac{5}{2}$ | -2 | -$\frac{5}{2}$ | -$\frac{10}{3}$ | $\frac{10}{3}$ | $\frac{5}{2}$ | 2 | $\frac{5}{2}$ | ΓΓ$\frac{10}{3}$ | Γ≠ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
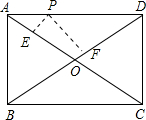 »γΆΦΘ§ΒψP «ΨΊ–ΈABCDΒΡ±ΏAD…œΒΡ“ΜΕ·ΒψΘ§ΨΊ–ΈΒΡΝΫΧθ±ΏABΓΔBCΒΡ≥ΛΖ÷±π «6ΚΆ8Θ§‘ρΒψPΒΫΨΊ–ΈΒΡΝΫΧθΕ‘Ϋ«œΏΨύάκ÷°ΚΆPE+PF «Θ®ΓΓΓΓΘ©
»γΆΦΘ§ΒψP «ΨΊ–ΈABCDΒΡ±ΏAD…œΒΡ“ΜΕ·ΒψΘ§ΨΊ–ΈΒΡΝΫΧθ±ΏABΓΔBCΒΡ≥ΛΖ÷±π «6ΚΆ8Θ§‘ρΒψPΒΫΨΊ–ΈΒΡΝΫΧθΕ‘Ϋ«œΏΨύάκ÷°ΚΆPE+PF «Θ®ΓΓΓΓΘ©| AΘ° | 4.8 | BΘ° | 5 | CΘ° | 6 | DΘ° | 7.2 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com