
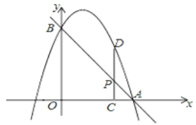
【题目】如图,已知抛物线![]() 分别交x轴、y轴于点A(2,0)、B(0,4),点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
分别交x轴、y轴于点A(2,0)、B(0,4),点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
(1)若![]() .
.
①求抛物线的解析式;
②当线段PD的长度最大时,求点P的坐标;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
【答案】(1) ①y=-2x2+2x+4;②P的坐标是(1,2); (2)见解析.
【解析】
(1)①把A、B的坐标代入抛物线解析式,由a+b=0,解方程组即可得出结论;
②设直线AB的解析式为![]() ,把A的坐标代入即可求出k的值,从而得到直线AB的解析式.设P点坐标为(m,﹣2m+4),则D(m,-2m2+2m+4),可表示出PD的长,利用二次函数的性质即可得出结论;
,把A的坐标代入即可求出k的值,从而得到直线AB的解析式.设P点坐标为(m,﹣2m+4),则D(m,-2m2+2m+4),可表示出PD的长,利用二次函数的性质即可得出结论;
(2)如图2,利用勾股定理计算出AB的长,再求出P的坐标,则可计算出PB的长,接着表示出抛物线解析式为y=ax2﹣2(a+1)x+4,则可用a表示出点D坐标为(1,2﹣a),所以PD=﹣a,由于∠DPB=∠OBA,根据相似三角形的判定方法,当![]() 时,△PDB∽△BOA,即
时,△PDB∽△BOA,即![]() ;当
;当![]() 时,△PDB∽△BAO,即
时,△PDB∽△BAO,即![]() ,然后解方程分别求出a的值,从而得到对应的抛物线的解析式.
,然后解方程分别求出a的值,从而得到对应的抛物线的解析式.
(1)①把A(2,0)、B(0,4)代入![]() 得:
得:![]() .
.
∵a+b=0,∴
∴![]() ,∴抛物线的解析式为y=-2x2+2x+4;
,∴抛物线的解析式为y=-2x2+2x+4;
②设直线AB的解析式为![]() ,则
,则![]() ,∴
,∴![]() ,∴直线AB的解析式为
,∴直线AB的解析式为![]() .
.
设P点坐标为(m,﹣2m+4),则D(m,-2m2+2m+4),∴PD=﹣2m2+2m+4﹣(﹣2m+4)=﹣2m2+4m![]() ,∴当
,∴当![]() 时,线段PD的长度最大,此时点P的坐标是(1,2).
时,线段PD的长度最大,此时点P的坐标是(1,2).
(2)存在.
如图2,OB=4,OA=2,则AB=![]() =2
=2![]() .
.
当x=1时,y=﹣2x+4=2,则P(1,2),∴PB=![]() =
=![]() .
.
把A(2,0)代入y=ax2+bx+4得4a+2b+4=0,解得:b=-2a-2,∴抛物线的解析式为y=ax2-2(a+1)x+4.
当x=1时,y=ax2-2(a+1)x+4=a-2a-2+4=2-a,则D(1,2-a),∴PD=2-a-2=﹣a.
∵DC∥OB,∴∠DPB=∠OBA.
当![]() 时,△PDB∽△BOA,即
时,△PDB∽△BOA,即![]() ,解得:a=-2,此时抛物线解析式为y=-2x2+2x+4;
,解得:a=-2,此时抛物线解析式为y=-2x2+2x+4;
当![]() 时,△PDB∽△BAO,即
时,△PDB∽△BAO,即![]() ,解得:a=-
,解得:a=-![]() ,此时抛物线解析式为y=-
,此时抛物线解析式为y=-![]() x2+3x+4.
x2+3x+4.
综上所述:满足条件的抛物线的解析式为y=﹣2x2+2x+4或y=-![]() x2+3x+4.
x2+3x+4.


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:
【题目】体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.

(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
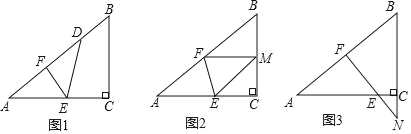
【题目】如图,已知一个三角形纸片ACB,其中∠ACB=90°,AC=8,BC=6,E、F分别是AC、AB边上的点,连接EF.(1)如图1,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=4S△EDF,求ED的长;
(2)如图2,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)如图3,若FE的延长线与BC的延长线交于点N,CN=2,CE=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
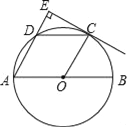
【题目】如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.
(1)求证:CE为⊙O的切线;
(2)判断四边形AOCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,則四辺形ABFD的周长为( )

A. 16cmB. 18cmC. 20cmD. 22cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面一元二次方程的解法中,正确的是( )
A. (x-3)(x-5)=10×2,∴x-3=10,x-5=2,∴x1=13,x2=7
B. (2-5x)+(5x-2)2=0,∴(5x-2)(5x-3)=0,∴x1=![]() ,x2=
,x2=![]()
C. (x+2)2+4x=0,∴x1=2,x2=-2
D. x2=x 两边同除以x,得x=1
查看答案和解析>>
科目:初中数学 来源: 题型:
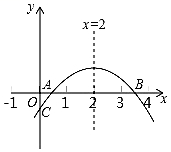
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴正半轴相交于A、B两点,与
轴正半轴相交于A、B两点,与![]() 轴相交于点C,对称轴为直线
轴相交于点C,对称轴为直线![]() 且OA=OC,则下列结论:①
且OA=OC,则下列结论:①![]() ②
②![]() ③
③![]() ④关于
④关于![]() 的方程
的方程![]() 有一个根为
有一个根为![]() 其中正确的结论个数有( )
其中正确的结论个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣3,4),B(﹣5,2),C(﹣2,1).
(1)画出△ABC绕原点O逆时针方向旋转90°得到的△A'B'C';并直接写出点A',B',C'的坐标:A' ,B' ,C' .
(2)在(1)的条件下,求在旋转的过程中,点A所经过的路径长,(结果保留π)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com