
 相似三角形面积的比等于相似比的平方,相似多边形面积之比等于相似比的平方.
相似三角形面积的比等于相似比的平方,相似多边形面积之比等于相似比的平方.分析 直接利用相似三角形的性质结合相似三角形判定方法得出答案.
解答 解:相似三角形面积的比等于 相似比的平方,相似多边形面积之比等于 相似比的平方.
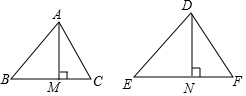
如图,因为△ABC∽△DEF,相似比为k,
所以∠B=∠E,$\frac{AB}{DE}$=$\frac{BC}{EF}$=k.
因为AM⊥BC,DN⊥EF,
所以∠AMB=∠DNE=90°
所以△ABM∽△DEN( 两角相等的三角形相似)
所以$\frac{AB}{DE}$=$\frac{AM}{DN}$=k
因为S△ABC=$\frac{1}{2}$BC•AM,S△DEF=$\frac{1}{2}$EF•DN,
所以$\frac{{S}_{△ABC}}{{S}_{△DEF}}$=k2.
故答案为:相似比的平方,相似比的平方,E,k,DEN,90°,DEN,两角相等的三角形相似,k,k2.
点评 此题主要考查了相似图形,正确把握相似三角形的判定与性质是解题关键.


科目:初中数学 来源: 题型:解答题
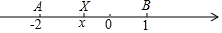 我们知道一个数x的绝对值的几何意义是:在数轴上表示这个数x的点离原点(表示数0)的距离,x的绝对值表示为|x|,也可以写成|x-0|,比如|2|=|2-0|=2;
我们知道一个数x的绝对值的几何意义是:在数轴上表示这个数x的点离原点(表示数0)的距离,x的绝对值表示为|x|,也可以写成|x-0|,比如|2|=|2-0|=2;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
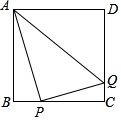 如图,正方形ABCD的边长为4,点P为BC边上的动点,连接AP,作PQ⊥AP,交CD于点Q,连接AQ,当点P从B点运动到C点时,线段AQ的中点所经过的路径长为1.
如图,正方形ABCD的边长为4,点P为BC边上的动点,连接AP,作PQ⊥AP,交CD于点Q,连接AQ,当点P从B点运动到C点时,线段AQ的中点所经过的路径长为1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
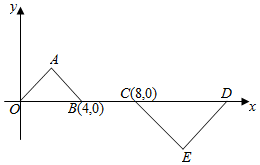 如图所示,等腰直角三角形OAB和等腰直角三角形CDE是位似图形,点A的坐标为(2,2),点E的坐标为(12,-4),则这两个等腰直角三角形的位似中心的坐标为($\frac{16}{3}$,0).
如图所示,等腰直角三角形OAB和等腰直角三角形CDE是位似图形,点A的坐标为(2,2),点E的坐标为(12,-4),则这两个等腰直角三角形的位似中心的坐标为($\frac{16}{3}$,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com