
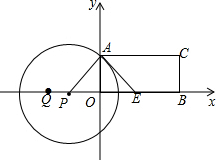
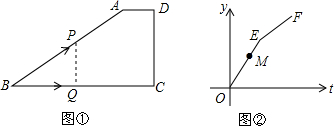
 如图,矩形ABCD,A(0,3)、B(6,0),点E在OB上,∠AEO=45°,点P从点Q(-4,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t秒.
如图,矩形ABCD,A(0,3)、B(6,0),点E在OB上,∠AEO=45°,点P从点Q(-4,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t秒.分析 (1)由A,B的坐标及∠AEO=45°可得出点E的坐标为(3,0);
(2)分为两种情况:①当P在点E的左侧时,②当P在点E的右侧时,分别求出t的值,
(3)本小题分三种情况讨论:①当PA⊥AE时,⊙P与AE相切;②当PA⊥AC时,⊙P与AC相切;③当PB⊥BC时,⊙P与BC相切;分别求出各种情况的t的值.
解答 解:(1)∵A(0,3),B(6,0),
∴OA=3,OB=6,
∵∠AEO=45°,
∴OE=OA=3,
∴点E的坐标(3,0);
(2)①当P在点E的左侧时,
∵∠AEO=45°,
∴∠EAO=45°,∵∠PAE=15°
∴∠OAP=∠EAO-∠PAE=45°-15°=30°,
∵AO=3,
∴OP=$\frac{\sqrt{3}}{3}$AO=$\sqrt{3}$,
∵Q(-4,0),
∴QP=$\sqrt{3}$+4,
∵点P沿x轴向右以每秒1个单位的速度运动,
∴t=$\sqrt{3}$+4,
②当P在点B的右侧时,
∵∠EAO=45°,∠PAE=15°
∴∠OAP=∠EAO+∠PAE=45°+15°=60°,
∵AO=3,
∴OP=$\sqrt{3}$AO=3$\sqrt{3}$,
∵Q(-4,0),
∴QP=3$\sqrt{3}$+4,
∵点P沿x轴向右以每秒1个单位的速度运动,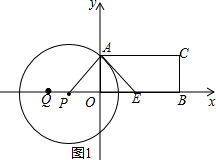
∴t=3$\sqrt{3}$+4,
综上所述当∠PAE=15°时,t的值为$\sqrt{3}$+4或3$\sqrt{3}$+4;
(3)①如图1,当PA⊥AE时,⊙P与AE相切,
∵∠EAO=45°,
∴∠APE=45°,AP=AE,
∵AO=3,
∴PO=3,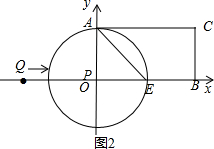
∴QP=QO-PO=4-3=1,
∵点P从点Q(-4,0)出发,沿x轴向右以每秒1个单位的速度运动,
∴t=1(秒),
②如图2,当PA⊥AC时,⊙P与AC相切,
∵QO=4,点P从点Q(-4,0)出发,沿x轴向右以每秒1个单位的速度运动,
∴t=4(秒),
③如图3,当PB⊥BC时,⊙P与BC相切,设PB=r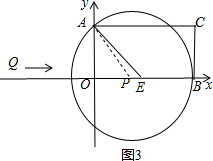 ∵OB=6,OA=3,
∵OB=6,OA=3,
∴OP2+OA2=PA2,即(6-r)2+32=r2,解得:r=$\frac{15}{4}$,
∴QP=4+5-$\frac{15}{4}$=$\frac{25}{4}$,
∵点P从点Q(-4,0)出发,沿x轴向右以每秒个单位的速度运动,
∴t=$\frac{25}{4}$,
综上所述t1=1秒,t2=4秒,t3=$\frac{25}{4}$秒.
点评 本题主要考查了圆的综合题,切线的性质,矩形的性质,图形的性质,解题的关键是分类讨论当⊙P与四边形OBCA的边(或边所在直线)相切的三种情况.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
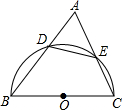 如图,在锐角△ABC中,以BC为直径的半圆O分别交AB,AC于D,E两点,且cosA=$\frac{\sqrt{3}}{3}$,则S△ADE:S四边形DBCE的值为$\frac{1}{2}$.
如图,在锐角△ABC中,以BC为直径的半圆O分别交AB,AC于D,E两点,且cosA=$\frac{\sqrt{3}}{3}$,则S△ADE:S四边形DBCE的值为$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x-3y=5}\\{2x+y=5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x-y=5}\\{x+y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y=x-3}\\{y-2x=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2y}\\{x=3y+1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 3 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相交,相交 | B. | 平行,平行 | C. | 平行,垂直相交 | D. | 垂直相交,平行 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com