
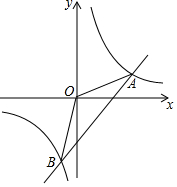
 如图,在平面直角坐标系中,不经过原点的直线与双曲线y=$\frac{k}{x}$相交于点A(m,3),B(-2,n),其中m>0,n<0
如图,在平面直角坐标系中,不经过原点的直线与双曲线y=$\frac{k}{x}$相交于点A(m,3),B(-2,n),其中m>0,n<0分析 (1)把点A(m,3),B(-2,n)在双曲线y=$\frac{k}{x}$上,即可得到结论;
(2)由点A(m,3),B(-2,n),得到OA2=m2+9=$\frac{4}{9}$n2+9,OB2=n2+4,根据已知条件得到$\frac{4}{9}$n2+9=$\frac{5}{8}$(n2+4),求得n=-6,m=4,即可得到结论.
解答 解:(1)∵点A(m,3),B(-2,n)在双曲线y=$\frac{k}{x}$上,
∴3m=-2n,
∴m=-$\frac{2}{3}$n;
(2)∵点A(m,3),B(-2,n),
∴OA2=m2+9=$\frac{4}{9}$n2+9,OB2=n2+4,
∵OA=$\frac{\sqrt{10}}{4}$OB,
∴OA2=$\frac{5}{8}$OB2,
即:$\frac{4}{9}$n2+9=$\frac{5}{8}$(n2+4),
∴n=±6,
∵n<0,
∴n=-6,
∴m=4,
∴k=12,
∴反比例函数的解析式为y=$\frac{12}{x}$,
设直线的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{3=4k+b}\\{-6=-2k+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=\frac{3}{2}}\\{b=-3}\end{array}\right.$,
∴直线的解析式为y=$\frac{3}{2}$x-3.
点评 本题考查了反比例函数与一次函数的交点,待定系数法求函数的解析式,解题的关键是熟练运用待定系数法,本题属于中等题型.


科目:初中数学 来源: 题型:解答题
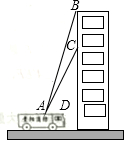 贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).
贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①、②是真命题 | B. | ②、③是真命题 | C. | ①、③是假命题 | D. | 以上结论都错 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,不经过原点的直线与双曲线y=$\frac{k}{x}$相交于点A(m,2),B(n,-1),其中m>0,n<0.
如图,在平面直角坐标系xOy中,不经过原点的直线与双曲线y=$\frac{k}{x}$相交于点A(m,2),B(n,-1),其中m>0,n<0.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{6}{3x}$ | B. | $\frac{4x}{{x}^{2}+3x}$ | C. | $\frac{x+2}{{x}^{2}+4}$ | D. | $\frac{3-x}{x-3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com