
 斐波那契(约1170-1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果,在实际生活中,很多花朵(如梅花,飞燕草,万寿菊等)的瓣数恰是斐波那契数列中的数,斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.斐波那契数列中的第n个数可以用$\frac{1}{\sqrt{5}}$[($\frac{1+\sqrt{5}}{2}$)n-($\frac{1-\sqrt{5}}{2}$)n]表示.
斐波那契(约1170-1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果,在实际生活中,很多花朵(如梅花,飞燕草,万寿菊等)的瓣数恰是斐波那契数列中的数,斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.斐波那契数列中的第n个数可以用$\frac{1}{\sqrt{5}}$[($\frac{1+\sqrt{5}}{2}$)n-($\frac{1-\sqrt{5}}{2}$)n]表示.分析 分别把1、2代入式子化简求得答案即可.
解答 解:第1个数,当n=1时,$\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^{n}-(\frac{1-\sqrt{5}}{2})^{n}]$
=$\frac{1}{\sqrt{5}}(\frac{1+\sqrt{5}}{2}-\frac{1-\sqrt{5}}{2})$
=$\frac{1}{\sqrt{5}}×\sqrt{5}$
=1.
第2个数,当n=2时,$\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^{n}-(\frac{1-\sqrt{5}}{2})^{n}]$
=$\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^{2}-(\frac{1-\sqrt{5}}{2})^{2}]$
=$\frac{1}{\sqrt{5}}×(\frac{1+\sqrt{5}}{2}+\frac{1-\sqrt{5}}{2})×(\frac{1+\sqrt{5}}{2}-\frac{1-\sqrt{5}}{2})$
=$\frac{1}{\sqrt{5}}×1×\sqrt{5}$
=1,
故答案为:1,1
点评 此题考查二次根式的混合运算与化简求值,理解题意,找出运算的方法是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
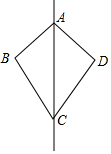 如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为( )
如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为( )| A. | 55° | B. | 65° | C. | 75° | D. | 85° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y3<y2 | B. | y2<y1<y3 | C. | y3<y2<y1 | D. | y3<y1<y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 50° | B. | 80° | C. | 50°或80° | D. | 25°或65° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com