
 如图所示,两个完全相同的直角梯形重叠在一起,将其中一个直角梯形沿平移,阴影部分的面积为140cm2.
如图所示,两个完全相同的直角梯形重叠在一起,将其中一个直角梯形沿平移,阴影部分的面积为140cm2. 分析 根据平移的性质得S梯形ABCD=S梯形EFGH,BC=FG=20,则FQ=FG-QG=15,S阴影部分=S梯形BCQF,然后根据梯形的面积公式求解即可.
解答 解: 如图,
如图,
∵梯形ABCD平移到梯形EFGH的位置,
∴S梯形ABCD=S梯形EFGH,BC=FG=20,
∴FQ=FG-QG=20-5=15,S阴影部分=S梯形BCQF,
而S梯形BCQF=$\frac{1}{2}$×(15+20)×8=140,
∴S阴影部分=140cm2.
故答案为140cm2.
点评 本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.也考查了梯形的面积公式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 甲-M,乙-N,丙-P | B. | 甲-M,乙-P,丙-N | C. | 甲-N,乙-P,丙-M | D. | 甲-P,乙-N,丙-M |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
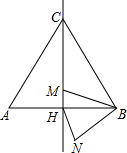 如图,边长为5的等边三角形ABC中,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是1.25.
如图,边长为5的等边三角形ABC中,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是1.25.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,?ABCD中,AC⊥AB,AB=3cm,BC=5cm,点E为AB上一点,且AE=$\frac{1}{3}$AB.点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止.则当运动时间为$\frac{5}{3}$,2,$\frac{12}{5}$,$\frac{{68-2\sqrt{21}}}{5}$秒时,△BEP为等腰三角形.
如图,?ABCD中,AC⊥AB,AB=3cm,BC=5cm,点E为AB上一点,且AE=$\frac{1}{3}$AB.点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止.则当运动时间为$\frac{5}{3}$,2,$\frac{12}{5}$,$\frac{{68-2\sqrt{21}}}{5}$秒时,△BEP为等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
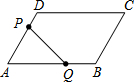 如图,在平行四边形ABCD中,AB=8cm,AD=4cm,∠A=60°,动点P以2cm/s的速度从D向点A移动,动点Q以4cm/s的速度从点A向点B移动.如果P、Q两点分别从D、A同时出发,当一方到达终点时都随之停止运动,那么经过1秒,五边形PQBCD面积最小.
如图,在平行四边形ABCD中,AB=8cm,AD=4cm,∠A=60°,动点P以2cm/s的速度从D向点A移动,动点Q以4cm/s的速度从点A向点B移动.如果P、Q两点分别从D、A同时出发,当一方到达终点时都随之停止运动,那么经过1秒,五边形PQBCD面积最小.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在数学活动中,我们得知三角点阵前n行的点数之和是1+2+3+…+n(n为正整数),这个结果可用公式$\frac{1}{2}$n(n+1)求得,如果这个结果是21,那么这个三角点阵的行数n是6.
如图,在数学活动中,我们得知三角点阵前n行的点数之和是1+2+3+…+n(n为正整数),这个结果可用公式$\frac{1}{2}$n(n+1)求得,如果这个结果是21,那么这个三角点阵的行数n是6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com