
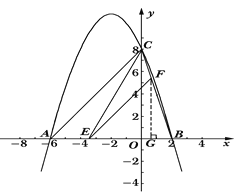
【题目】已知:二次函数![]() 的图象与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且A点坐标为(-6,0).
的图象与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且A点坐标为(-6,0).
(1)求此二次函数的表达式;
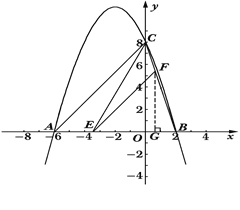
(2)若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
【答案】(1)y=-![]() x2-
x2-![]() x+8(2)
x+8(2)
【解析】试题分析:(1)求出一元二次方程的两根即可求出两点坐标,把B、C两点坐标代入二次函数的解析式就可解答;
(2)过点F作FG⊥AB,垂足为G,由EF∥AC,得△BEF∽△BAC,利用相似比求EF,利用sin∠FEG=sin∠CAB求FG,根据S=S△BCE-S△BFE,求S与m之间的函数关系式.
解:(1)解方程x2-10x+16=0得x1=2,x2=8
∴B(2,0)、C(0,8)
∴所求二次函数的表达式为y=-![]() x2-
x2-![]() x+8
x+8
(2)∵AB=8,OC=8,依题意,AE=m,则BE=8-m,
∵OA=6,OC=8, ∴AC=10.
∵EF∥AC, ∴△BEF∽△BAC.
∴![]() =
=![]() . 即
. 即![]() =
=![]() . ∴EF=
. ∴EF=![]() .
.
过点F作FG⊥AB,垂足为G,
则sin∠FEG=sin∠CAB=![]() .∴
.∴![]() =
=![]() .
.
∴FG=![]() ·
·![]() =8-m.
=8-m.
∴S=S△BCE-S△BFE
=![]()
![]() (0<m<8)
(0<m<8)
点睛:本题考查了一元二次方程的解法,待定系数法求函数关系系,相似三角形的判定与性质,span>锐角三角函数的定义,割补法求图形的面积,熟练掌握待定系数法求二次函数关系式、相似三角形的判定与性质是解答本题的关键.
【题型】解答题
【结束】
23
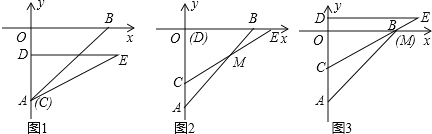
【题目】如图(1),在平面直角坐标系中,点A(0,﹣6),点B(6,0).Rt△CDE中,∠CDE=90°,CD=4,DE=4![]() ,直角边CD在y轴上,且点C与点A重合.Rt△CDE沿y轴正方向平行移动,当点C运动到点O时停止运动.解答下列问题:
,直角边CD在y轴上,且点C与点A重合.Rt△CDE沿y轴正方向平行移动,当点C运动到点O时停止运动.解答下列问题:
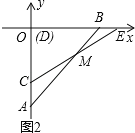
(1)如图(2),当Rt△CDE运动到点D与点O重合时,设CE交AB于点M,求∠BME的度数.
(2)如图(3),在Rt△CDE的运动过程中,当CE经过点B时,求BC的长.
(3)在Rt△CDE的运动过程中,设AC=h,△OAB与△CDE的重叠部分的面积为S,请写出S与h之间的函数关系式,并求出面积S的最大值.
【答案】(1)∠BME=15°;
(2BC=4![]() ;
;
(3)h≤2时,S=﹣![]() h2+4h+8,
h2+4h+8,
当h≥2时,S=18﹣3h.
【解析】
试题分析:(1)如图2,由对顶角的定义知,∠BME=∠CMA,要求∠BME的度数,需先求出∠CMA的度数.根据三角形外角的定理进行解答即可;
(2)如图3,由已知可知∠OBC=∠DEC=30°,又OB=6,通过解直角△BOC就可求出BC的长度;
(3)需要分类讨论:①h≤2时,如图4,作MN⊥y轴交y轴于点N,作MF⊥DE交DE于点F,S=S△EDC﹣S△EFM;②当h≥2时,如图3,S=S△OBC.
试题解析:解:(1)如图2,
∵在平面直角坐标系中,点A(0,﹣6),点B(6,0).
∴OA=OB,
∴∠OAB=45°,
∵∠CDE=90°,CD=4,DE=4![]() ,
,
∴∠OCE=60°,
∴∠CMA=∠OCE﹣∠OAB=60°﹣45°=15°,
∴∠BME=∠CMA=15°;
如图3,
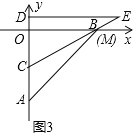
∵∠CDE=90°,CD=4,DE=4![]() ,
,
∴∠OBC=∠DEC=30°,
∵OB=6,
∴BC=4![]() ;
;
(3)①h≤2时,如图4,作MN⊥y轴交y轴于点N,作MF⊥DE交DE于点F,
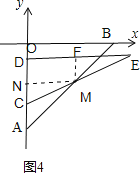
∵CD=4,DE=4![]() ,AC=h,AN=NM,
,AC=h,AN=NM,
∴CN=4﹣FM,AN=MN=4+h﹣FM,
∵△CMN∽△CED,
∴![]() ,
,
∴![]() ,
,
解得FM=4﹣![]() ,
,
∴S=S△EDC﹣S△EFM=![]() ×4×4
×4×4![]() ﹣
﹣![]() (4
(4![]() 4﹣h)×(4﹣
4﹣h)×(4﹣![]() )=﹣
)=﹣![]() h2+4h+8,
h2+4h+8,
②如图3,当h≥2时,
S=S△OBC=![]() OC×OB=
OC×OB=![]() (6﹣h)×6=18﹣3h.
(6﹣h)×6=18﹣3h.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】已知:Rt△A′BC′≌Rt△ABC,∠A′C′B=∠ACB=90°,∠A′BC′=∠ABC=60°,Rt△A′BC′可绕点B旋转,设旋转过程中直线CC′和AA′相交于点D.
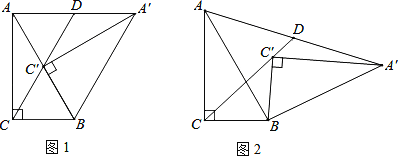
(1)如图1所示,当点C′在AB边上时,判断线段AD和线段A′D之间的数量关系,并证明你的结论;
(2)将Rt△A′BC′由图1的位置旋转到图2的位置时,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)将Rt△A′BC′由图1的位置按顺时针方向旋转α角(0°≤α≤120°),当A、C′、A′三点在一条直线上时,请直接写出旋转角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若数轴上![]() 两点分别对应实数
两点分别对应实数![]() ,则
,则![]() 两点之间的距离记作
两点之间的距离记作![]() ,且
,且![]() .已知点
.已知点![]() 在数轴上对应数字
在数轴上对应数字![]() 、点
、点![]() 在数轴上对应数字
在数轴上对应数字![]() 、点
、点![]() 在数轴上对应数字
在数轴上对应数字![]() 、点
、点![]() 在数轴上对应数字
在数轴上对应数字![]() 、点
、点![]() 在数轴上对应数字
在数轴上对应数字![]() .根据信息完成下列各题:
.根据信息完成下列各题:
(1)![]() =_____________.
=_____________.
(2)若数轴上点![]() 对应实数
对应实数![]() ,则
,则
①当![]() 时
时![]() =_____________;
=_____________;
②当![]() 取最小值时,
取最小值时,![]() 的取值范围为_____________.
的取值范围为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
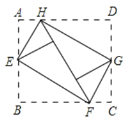
【题目】如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是________ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
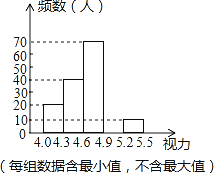
【题目】某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
(1)在频数分布表中,a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,O,B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.
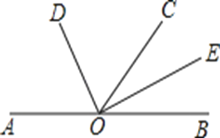
(1)若∠BOC=62°,求∠DOE的度数;
(2)若∠BOC=α,求∠DOE的度数;
(3)通过(1)(2)的计算,你能总结出什么结论,直接简写出来,不用说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划购进甲、乙两种商品共1200件,这两种商品的进价,售价如下表:
进价(元/件) | 售价(元/件) | |
甲 | 25 | 30 |
乙 | 45 | 60 |
(1)超市如何进货,进货款恰好为46000元;
(2)为确保乙商品畅销,在(1)的条件下,商家决定对乙商品进行打折出售,且全部售完后,乙商品的利润率为20%,请问乙商品需打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
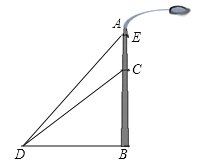
【题目】如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com