
【题目】如图所示,动点A,B同时从原点O出发,运动的速度都是每秒1个单位,动点A沿x轴正方向运动,动点B沿y轴正方向运动,以OA,OB为邻边建立正方形OACB,抛物线y=﹣x2+bx+c经过B,C两点,假设A,B两点运动的时间为t秒: 根据
根据
(1)直接写出直线OC的解析式;
(2)当t=3秒时,求此时抛物线的解析式;此时抛物线上是否存在一点D,使得S△BCD=6?若存在,求出点D的坐标;若不存在,说明理由;
(3)在(2)的条件下,有一条平行于y轴的动直线l,交抛物线于点E,交直线OC于点F,若以O、B、E、F四个点构成的四边形是平行四边形,求点F的坐标;
(4)在动点A、B运动的过程中,若正方形OACB内部有一个点P,且满足OP= ![]() ,CP=2,∠OPA=135°,直接写出此时AP的长度.
,CP=2,∠OPA=135°,直接写出此时AP的长度.
【答案】
(1)解:∵四边形OABC是正方形,
∴∠AOC=45°,
∴直线OC的解析式为y=x
(2)解:∵t=3秒,
∴OA=OB=3,
∴点B(0,3),C(3,3),
将点B、C代入抛物线得, ![]() ,
,
解得 ![]() ,
,
∴抛物线解析式为y=﹣x2+3x+3,
设BC边上的高为h,
∵BC=OA=3,S△BCD=6,
∴h=4,
∴点D的纵坐标为3﹣4=﹣1,
令y=﹣1,则﹣x2+3x+3=﹣1,
整理得,x2﹣3x﹣4=0,
解得x1=﹣1,x2=4,
所以,D1(﹣1,﹣1),D2(4,﹣1)
(3)解:∵OB=3,
∴EF=3,
设E(m,﹣m2+3m+3),F(m,m),
若E在F上方,则,﹣m2+3m+3﹣m=3,
整理得,m2﹣2m=0,
解得m1=0(舍去),m2=2,
∴F1(2,2),
若F在E上方,则,m﹣(﹣m2+3m+3)=3,
整理m2﹣2m﹣6=0,
解得m1=1﹣ ![]() ,m2=1+
,m2=1+ ![]() ,
,
∴F2(1﹣ ![]() ,1﹣
,1﹣ ![]() ),
),
F3(1+ ![]() ,1+
,1+ ![]() )
)
(4)解:如图,将△AOP绕点A逆时针旋转90°得到△AP′C,
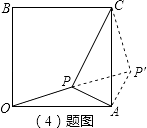
由旋转的性质得,AP′=AP,P′C=OP= ![]() ,∠AP′C=∠OPA=135°,
,∠AP′C=∠OPA=135°,
∵△APP′是等腰直角三角形,
∴∠AP′P=45°,
∴∠PP′C=135°﹣45°=90°,
由勾股定理得,PP′= ![]() =
= ![]() =
= ![]() ,
,
所以,AP= ![]() PP′=
PP′= ![]() ×
× ![]() =1.
=1.
【解析】(1)由正方形的性质得出∠AOC=45°。易得直线OC的解析式为y=x.
(2)根据已知求出点B、C两点的坐标,用待定系数法就可以求出二次函数的解析式。设BC边上的高为h,根据三角形的面积求出h的值,即可求出点D的纵坐标,将点D的纵坐标代入函数解析式就可以 求出点D的坐标。
(3)已知O、B、E、F四个点构成的四边形是平行四边形,则有OB=EF=3,点E在抛物线上,点F在直线y=x上,分两种情况:点E在点F的上方;点E在点F的下方,设出点E、F的坐标,根据OB=EF,建立方程求解,即可求出点F的坐标。
(4)此题用旋转的知识来解答。将△AOP绕点A逆时针旋转90°得到△AP′C,易证明APP′是等腰直角三角形,再求出∠PP′C=90°,利用勾股定理就可以求出AP的长。
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对平行四边形的性质的理解,了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


科目:初中数学 来源: 题型:
【题目】如图,线段AB=10,点P在线段AB上,在AB的同侧分别以AP,BP为边长作正方形APCD和BPEF,点M、N分别是EF、CD的中点,则MN的最小值是 . 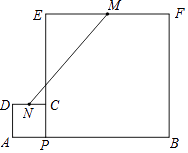
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 CB 和射线 OA,CB//OA,点 B 在点 C 的右侧.且满足∠OCB=∠OAB=100°,连接线段 OB,点 E、F 在直线 CB 上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠BOE
(2)当点 E、F 在线段 CB 上时(如图 1),∠OEC 与∠OBA 的和是否是定值?若是,求出这个值;若不是,说明理由。
(3)如果平行移动 AB,点 E、F 在直线 CB 上的位置也随之发生变化.当点 E、F 在点 C 左侧时,∠OEC 和∠OBA 之间的数量关系是否发生变化?若不变,说明理由;若变化,求出他们之间的关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:数学兴趣小组在活动时,老师提出了这样一个问题:如图①,在Rt△ABC中,∠BAC=90°,BC=10,AD是BC边上的中线,求AD的长度.小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,则AD=![]() AE
AE

在△ADC和△EDB中

∴△ADC≌△EDB
∴∠DBE=∠DCA,BE=AC
∴BE∥AC
∴∠EBA+∠BAC=180°
∵∠BAC=90°
∴∠EBA=90°
在△EBA和△CAB中

∴△EBA≌△CAB
∴AE=BC
∵BC=10
∴AD=![]() AE=
AE=![]() BC=5
BC=5
(1)若将上述问题中条件“BC=10”换成“BC=a”,其他条件不变,则可得AD= .
从上得到结论:直角三角形斜边上的中线,等于斜边的一半.
(感悟)解题时,条件中若出现“中点”“中线”等字样,可以考虑延长中线构造全等三角形进而求解.
问题解决:(2)如图②,在四边形ABCD中,AD∥BC,∠D=90°,M是AB的中点.若CM=6.5,BC+CD+DA=17,求四边形ABCD的面积.
问题拓展:(3)如图③,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,∠DFE与∠AEF的度数满足数量关系:∠DFE=k∠AEF,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某生物兴趣小组在四天的试验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同.他们将一头骆驼前两昼夜的体温变化情况绘制成如图所示的图象,请根据图象完成下列问题:
(1)第一天中,在什么时间范围内这头骆驼的体温是上升的?它的体温从最低上升到最高需要多长时间?
(2)第三天12时这头骆驼的体温是多少?
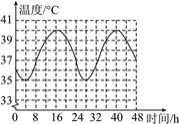
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司现有114吨货物,计划同时租出A,B两种型号的车,王经理发现一个运货货单上的一个信息是:
A型车(满载) | B型车(满载) | 运货总量 |
3辆 | 2辆 | 38吨 |
1辆 | 3辆 | 36吨 |
根据以上信息,解析下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)若物流公司打算一次运完,且恰好每辆车都装满货物,请你帮该物流公司设计租车方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以![]() 等为代表的战略性新兴产业.据统计,目前广东
等为代表的战略性新兴产业.据统计,目前广东![]() 基站的数量约
基站的数量约![]() 万座,计划到2020年底,全省
万座,计划到2020年底,全省![]() 基站数量是目前的
基站数量是目前的![]() 倍,到2022年底,全省
倍,到2022年底,全省![]() 基站数量将达到
基站数量将达到![]() 万座.
万座.
![]() 计划到2020年底,全省
计划到2020年底,全省![]() 基站的数量是多少万座?
基站的数量是多少万座?
![]() 按照计划,求2020年底到2022年底,全省
按照计划,求2020年底到2022年底,全省![]() 基站数量的年平均增长率;
基站数量的年平均增长率;
![]() 求2021年底全省
求2021年底全省![]() 基站的数量.
基站的数量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com