
【题目】在平面直角坐标系xOy中,图形G的投影矩形定义如下:矩形的两组对边分别平行于x轴,y轴,图形G的顶点在矩形的边上或内部,且矩形的面积最小.设矩形的较长的边与较短的边的比为k,我们称常数k为图形G的投影比.如图1,矩形ABCD为△DEF的投影矩形,其投影比![]() .
.
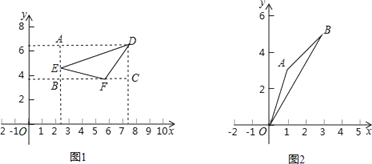
(1)如图2,若点A(1,3),B(3,5),则△OAB投影比k的值为 .
(2)已知点C(4,0),在函数y=2x﹣4(其中x<2)的图象上有一点D,若△OCD的投影比k=2,求点D的坐标.
(3)已知点E(3,2),在直线y=x+1上有一点F(5,a)和一动点P,若△PEF的投影比1<k<2,则点P的横坐标m的取值范围 (直接写出答案).
【答案】(1) ![]() ;(2) D(1,﹣2);(3) 1<m<3或m>5.
;(2) D(1,﹣2);(3) 1<m<3或m>5.
【解析】试题分析:(1)分别过点B作坐标轴的垂线,构成的矩形即是△OAB的投影矩形;(2)分类讨论,当点O,D,C都在投影矩形的边上时,点D在第四象限,当点D,C在投影矩形的边上,O在投影矩形内部时,点D在第三象限,然后利用投影比的定义求解;(3)点E,F是两个定点,点P是直线![]() 上的动点,根据点P的位置的不同,所构造的投影矩形也不同,所以应分三种情况讨论。
上的动点,根据点P的位置的不同,所构造的投影矩形也不同,所以应分三种情况讨论。
试题解析:(1)在图2中

过点B作BC⊥x轴于点C,作BD⊥y轴于点D,则矩形OCBD为△OAB的投影矩形,∵点B(3,5),∴OC=3,BC=5,∴△OAB投影比k的值为![]() =
=![]() .
.
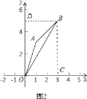
(2)∵点D为函数y=2x﹣4(其中x<2)的图象上的点,设点D坐标为(x,2x﹣4)(x<2).分以下两种情况:①当0≤x≤2时,如图3所示,
作投影矩形OMNC.∵OC≥OM,∴![]() ,解得x=1,∴D(1,﹣2);②当x<0时,如图4所示,作投影矩形MDNC.
,解得x=1,∴D(1,﹣2);②当x<0时,如图4所示,作投影矩形MDNC.
∵点D坐标为(x,2x﹣4),点M点坐标为(x,0),∴DM=|2x﹣4|=4﹣2x,MC=4﹣x,∵x<0,∴DM>CM,∴![]() ,但此方程无解.
,但此方程无解.
∴当x<0时,满足条件的点D不存在.综上所述,点D的坐标为D(1,﹣2).
(3)令y=x+1中y=2,则x+1=2,解得:x=1.
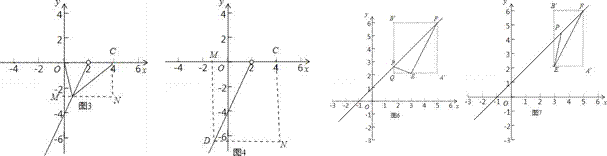
①当m≤1时,作投影矩形A′FB′P,如图5所示.此时点P(m,m+1),PA′=5﹣m,FA′=6﹣(m+1)=5﹣m,△PEF的投影比k=![]() =1,∴m≤1不符合题意;
=1,∴m≤1不符合题意;
②当1<m<3时,作投影矩形A′FB′Q,如图6所示.
此时点P(m,m+1),FB′=5﹣m,FA′=6﹣2=4,△PEF的投影比k=![]() =
=![]() ,
,
∵1<m<3,∴1<k<2,∴1<m<3符合题意;
③当3≤m≤5时,作投影矩形A′FB′E,如图7所示.
此时点E(3,2),FA′=6﹣2=4,FB′=5﹣3=2,△PEF的投影比k=![]() =2,
=2,
∴3≤m≤5不符合题意;
④当m>5时,作投影矩形A′PB′E,如图8所示.
此时点P(m,m+1),点E(3,2),![]() =
=![]() ,∵m>5,∴1<k<2,∴m>5符合题意.
,∵m>5,∴1<k<2,∴m>5符合题意.
综上可知:点P的横坐标m的取值范围为1<m<3或m>5.
故答案为:1<m<3或m>5.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】你知道为什么任何无限循环小数都可以写成分数形式吗?下面的解答过程会告诉 你原因和方法.
(1)阅读下列材料:
问题:利用一元一次方程将![]() 化成分数.
化成分数.
设 ![]() .
.
由![]() ,可知
,可知 ![]() ,
,
即 ![]() .(请你体会将方程两边都乘以10起到的作用)
.(请你体会将方程两边都乘以10起到的作用)
可解得 ![]() ,即
,即 ![]() .填空:将
.填空:将![]() 写成分数形式为 .
写成分数形式为 .
(2)请仿照上述方法把小数![]() 化成分数,要求写出利用一元一次方程进行解答的过程.
化成分数,要求写出利用一元一次方程进行解答的过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直角三角形的两条直角边分别为12cm和16cm,则这个直角三角形内切圆的半径是( )
A. 2cm B. 3cm C. 4cm D. 5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )
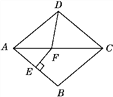
A. 80° B. 70° C. 65° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=(x-1)2+3向左平移1个单位,再向下平移3个单位所得抛物线的解析式为( )
A. y=x2 B. y=(x-2)2+6 C. y=x2+6 D. y=(x-2)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com