
分析 (1)假设恰好买100元的商品,正好送了50元,再添上50元正好购买了100元的商品,这时打折最多,由此利用实际消费的钱数除以购买商品的钱数得出答案即可;
(2)设王女士在该商场购买了商品B的价格为x元,购买商品的价格为x+480,实际消费480-200+x,根据优惠不超过8折,列出不等式解答即可.
解答 解:(1)(100+50)÷200
=150÷200
=75%.
答:这种优惠活动最多能打七五折.
(2)设王女士在该商场购买了商品B的价格为x元,由题意得
480-200+x≤80%(x+480)
解得:x≤520,
王女士在该商场至少消费480+520-200=800元.
答:王女士在该商场至少消费800元.
点评 此题考查一元一次不等式的实际运用,理解题意,掌握销售问题中的基本数量关系是解决问题的关键.


科目:初中数学 来源: 题型:解答题
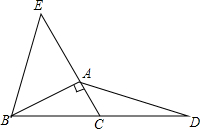 已知:如图,Rt△ABC中,∠BAC=90°,延长BC到点D,使CD=BC,延长CA到点E,使AE=2CA;连接AD,BE.求证:AD=BE.
已知:如图,Rt△ABC中,∠BAC=90°,延长BC到点D,使CD=BC,延长CA到点E,使AE=2CA;连接AD,BE.求证:AD=BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面坐标系中,点A(2,1)、B(6,2)、C(6,5)、D(2,4).
如图,在平面坐标系中,点A(2,1)、B(6,2)、C(6,5)、D(2,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
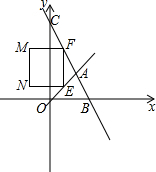 如图,在平面直角坐标系中,两个一次函数y=x,y=-2x+12的图象相交于点A,动点E从O出发,沿OA方向以每秒1个单位的速度运动,作EF∥y轴与直线BC交于点F,以EF为一边向x轴负方向作正方形EFMN,设正方形EFMN与△AOC的重叠部分的面积为S.
如图,在平面直角坐标系中,两个一次函数y=x,y=-2x+12的图象相交于点A,动点E从O出发,沿OA方向以每秒1个单位的速度运动,作EF∥y轴与直线BC交于点F,以EF为一边向x轴负方向作正方形EFMN,设正方形EFMN与△AOC的重叠部分的面积为S.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com