Question

今年，6月12日为端午节。在端午节前夕，三位同学到某超市调研一种进价为2元的粽子的销售情况。请根据小丽提供的信息，解答小华和小明提出的问题。

（1）小华的问题解答：　　　　；
（2）小明的问题解答：　　　　。

Answer 1

解：（1）当定价为4元时，能实现每天800元的销售利润。
（2）800元的销售利润不是最多，当定价为4.8元时，每天的销售利润最大。

解析试题分析：（1）设定价为x元，利润为y元，则销售量为：，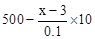
由题意得，。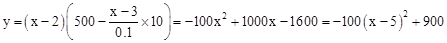
当y=800时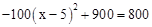，，解得：x=4或x=6。
∵售价不能超过进价的240%，∴x≤2×240%，即x≤4.8。∴x=4。
即小华问题的解答为：当定价为4元时，能实现每天800元的销售利润。
（2）由（1），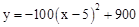
∵－100＜0，∴函数图象开口向下，且对称轴为x=5，
∵x≤4.8，∴当x=4.8时函数能取最大值，且。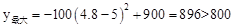
故小明的问题的解答为：800元的销售利润不是最多，当定价为4.8元时，每天的销售利润最大。