
 如图,在△ABC中,CD⊥AB于点D.下列条件:①BC2=BD•BA;②$\frac{AC}{AB}$=$\frac{AD}{AC}$;③CD2=AD•BD.其中能证明△ABC是直角三角形的是①②③.
如图,在△ABC中,CD⊥AB于点D.下列条件:①BC2=BD•BA;②$\frac{AC}{AB}$=$\frac{AD}{AC}$;③CD2=AD•BD.其中能证明△ABC是直角三角形的是①②③. 分析 首先把①③中的乘积式化成比例式,根据三角形相似的判定方法证出三角形相似,得出对应角相等,再运用角的互余关系得出∠ACB=90°即可;
②证明三角形相似,同理得出∠ACB=90°.
解答 解:∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∵BC2=BD•BA,
∴$\frac{BC}{BD}=\frac{BA}{BC}$,
又∵∠B=∠B,
∴△ABC∽△CBD,
∴∠A=∠BCD,
∵∠A+∠ACD=90°,
∴∠BCD+∠ACD=90°,
即∠ACB=90°,
∴①能证明△ABC是直角三角形;
∵$\frac{AC}{AB}$=$\frac{AD}{AC}$,∠A=∠A,
∴△ACD∽△ABC,
∴∠ACD=∠B,
∵∠ACD+∠ACD=90°,
∴∠A+∠B=90°,
∴∠ACB=90°,
即△ABC是直角三角形,
∴②能证明△ABC是直角三角形;
∵CD2=AD•BD,
∴$\frac{CD}{AD}=\frac{BD}{CD}$,
又∵∠ADC=∠BDC=90°,
∴△ACD∽△CBD,
∴∠ACD=∠B,
∴∠ACB=∠ACD+∠DCB=∠B+∠DCB=90°,
即△ABC是直角三角形,
∴③能证明△ABC是直角三角形;
综上所述:能证明△ABC是直角三角形的是①②③;
故答案为:①②③.
点评 本题考查了相似三角形的判定与性质、比例的性质、角的互余关系;熟练掌握相似三角形的判定与性质,证明三角形相似得出对应角相等是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日常语言 | 代数语言 |
| 一个商人有一笔钱 | x |
| 第一年他花去了100镑 | x-100 |
| 补进去余额的$\frac{1}{3}$ | (x-100)+$\frac{1}{3}$(x-100) |
| 第二年他又花去了100镑 | (1)(x-100)+$\frac{1}{3}$(x-100)-100 |
| 又补进去余额的$\frac{1}{3}$ | (2)(x-100)+$\frac{1}{3}$(x-100)-100+$\frac{1}{3}$[(x-100)+$\frac{1}{3}$(x-100)-100] |
| 结果他的钱数正好是原来的钱数 | (3)(x-100)+$\frac{1}{3}$(x-100)-100+$\frac{1}{3}$[(x-100)+$\frac{1}{3}$(x-100)-100]=x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
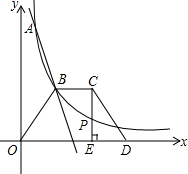 如图,一次函数y=k1x+b(k1≠0)与反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)(x>0)的图象交于A(1,6),B(a,3)两点,
如图,一次函数y=k1x+b(k1≠0)与反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)(x>0)的图象交于A(1,6),B(a,3)两点,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ax2=bx | B. | x2+3y-1=0 | C. | 3x2-2x+$\frac{1}{x}$=0 | D. | 2(x+1)(x-1)=x+5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com