
| A. | 1,-$\frac{1}{2}$ | B. | 1,-1 | C. | -1 | D. | $\frac{\sqrt{6}}{2}$,-$\frac{\sqrt{6}}{2}$ |
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{3}{2}$ | C. | -1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
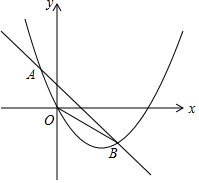 如图,在平面直角坐标系中,抛物线y=x2-bx与直线交于点A(-$\frac{1}{2}$,m),B(1,n),其中m>0,n<0,
如图,在平面直角坐标系中,抛物线y=x2-bx与直线交于点A(-$\frac{1}{2}$,m),B(1,n),其中m>0,n<0,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
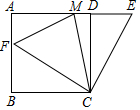 如图,四边形ABCD为正方形,边长为4,E为AD延长线上一点,DE=x(0<x<4),在AE上取一点M,连接CM,将△CME沿CM对折,若点E恰落在线段AB上的点F处,则AM=$\frac{8x}{4+x}$.
如图,四边形ABCD为正方形,边长为4,E为AD延长线上一点,DE=x(0<x<4),在AE上取一点M,连接CM,将△CME沿CM对折,若点E恰落在线段AB上的点F处,则AM=$\frac{8x}{4+x}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
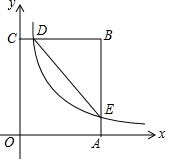 如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=$\frac{k}{x}$(k>0)的图象经过点D且与边BA交于点E,连接DE.
如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=$\frac{k}{x}$(k>0)的图象经过点D且与边BA交于点E,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学为响应2017年万州区委、区府喜迎世界读书日“全面阅读,书香万州”建设的号召,在全校形成良好的人文阅读,该中学随机调查了八年级部分学生平均每天的阅读时间,统计结果如图所示:
某中学为响应2017年万州区委、区府喜迎世界读书日“全面阅读,书香万州”建设的号召,在全校形成良好的人文阅读,该中学随机调查了八年级部分学生平均每天的阅读时间,统计结果如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 22 | B. | 21 | C. | 20 | D. | 19 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com