
 (2012•南充模拟)如图,有一块半圆形钢板,直径AB=20cm,计划将此钢板切割成下底为AB的等腰梯形,上底CD的端点在圆周上,且CD=10cm.求图中阴影部分的面积.
(2012•南充模拟)如图,有一块半圆形钢板,直径AB=20cm,计划将此钢板切割成下底为AB的等腰梯形,上底CD的端点在圆周上,且CD=10cm.求图中阴影部分的面积.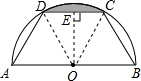 解:连接OC,OD,过点O作OE⊥CD于点E.
解:连接OC,OD,过点O作OE⊥CD于点E.| CO2-CE2 |
| 102-52 |
| 3 |
| 1 |
| 2 |
| 60π×102 |
| 360 |
| 50π |
| 3 |
| 1 |
| 2 |
| 3 |
| 50 |
| 3 |
| 3 |
| 50 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
 (2012•南充模拟)如图,现有一个圆心角为90°,半径为16cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为
(2012•南充模拟)如图,现有一个圆心角为90°,半径为16cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com