
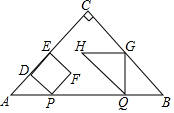
 ��ͼ����ABC�ǵ���ֱ�������Σ���ACB=90�㣬AB=4cm������P��1cm/s���ٶȷֱ�ӵ�A��Bͬʱ��������P��A��B���յ�B�˶�����Q��B��A���յ�A�˶�������P��PD��AC�ڵ�D����PDΪ�����Ҳ���������PDEF������Q��QG��AB��������BC-CA�ڵ�G���C���غϣ���QGΪ��������ֱ�ǡ�QGH���ҵ�GΪֱ�Ƕ��㣬��C��Hʼ����QG��ͬ�࣬��������PDEF���QGH�ص�����ͼ�ε����ΪS��cm2������P�˶���ʱ��Ϊt��s����0��t��4����
��ͼ����ABC�ǵ���ֱ�������Σ���ACB=90�㣬AB=4cm������P��1cm/s���ٶȷֱ�ӵ�A��Bͬʱ��������P��A��B���յ�B�˶�����Q��B��A���յ�A�˶�������P��PD��AC�ڵ�D����PDΪ�����Ҳ���������PDEF������Q��QG��AB��������BC-CA�ڵ�G���C���غϣ���QGΪ��������ֱ�ǡ�QGH���ҵ�GΪֱ�Ƕ��㣬��C��Hʼ����QG��ͬ�࣬��������PDEF���QGH�ص�����ͼ�ε����ΪS��cm2������P�˶���ʱ��Ϊt��s����0��t��4�������� ��1����ͼ1�У�����F�ڱ�QH��ʱ����֪AP=PQ=BQ�����AB�ij����ɽ�����⣻
��2��������������ͼ2�У�����F��GQ��ʱ����֪AP=BQ=t��PD=PF=$\frac{\sqrt{2}}{2}$t��PQ=PF=$\frac{1}{2}$t���г����̼��ɽ�����⣻����ͼ3�У��ص��������ı���GHRTʱ��
��3��������������������ͼ5�У���FH��ABʱ���ӳ�HF��AB��T����֪AP=BQ=GQ=HG=TQ=t��PT=$\frac{1}{2}$t������ͼ7�У���FH��ABʱ����֪AQ=PQ=$\frac{1}{2}$t��BQ=t���ֱ��г����̼��ɽ�����⣮����ͼ8�У���HF��ABʱ��
��� �⣺��1����ͼ1�У�����F�ڱ�QH��ʱ����֪AP=PQ=BQ��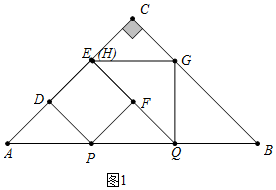
��Rt��ABC��AB=4��
��t=$\frac{4}{3}$ʱ����F�ڱ�QH�ϣ�
��2����ͼ2�У�����F��GQ��ʱ����֪AP=BQ=t��PD=PF=$\frac{\sqrt{2}}{2}$t��PQ=PF=$\frac{1}{2}$t��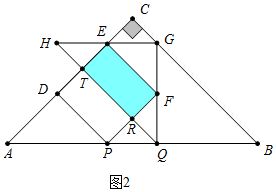
��t+$\frac{1}{2}$t+t=4��
��t=$\frac{8}{5}$��
�ɣ�1����֪����$\frac{4}{3}$��t��$\frac{8}{5}$ʱ��������PDEF���QGH�ص�����ͼ�����ı���
��ʱs=$\frac{\sqrt{2}}{2}$t•[$\frac{\sqrt{2}}{2}$t-$\frac{\sqrt{2}}{2}$��4-2t��]=$\frac{3}{2}$t2-2t��
��ͼ3�У���G��EF��ʱ������$\sqrt{2}$��4-t��=$\frac{\sqrt{2}}{2}$t+$\frac{\sqrt{2}}{2}$��2t-4�������t=$\frac{12}{5}$��
��ͼ4�У���G��D�غ�ʱ����֪2t-4=$\frac{1}{2}$t�����t=$\frac{8}{3}$��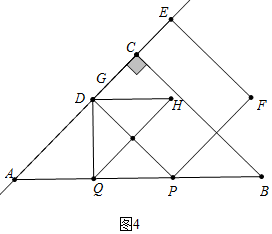
��$\frac{12}{5}$��t��$\frac{8}{3}$ʱ��S=S��GHQ-S��TRQ=$\frac{1}{2}$��4-t��2-$\frac{1}{2}$[$\frac{\sqrt{2}}{2}$��2t-4��]2=-$\frac{1}{2}$t2-4��
��3������ͼ5�У���FH��ABʱ���ӳ�HF��AB��T����֪AP=BQ=GQ=HG=TQ=t��PT=$\frac{1}{2}$t��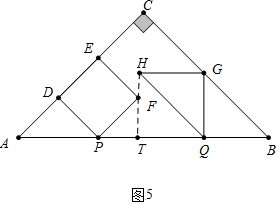
��3t+$\frac{1}{2}$t=4��
��t=$\frac{8}{7}$��
����ͼ7�У���HF��AB��Tʱ��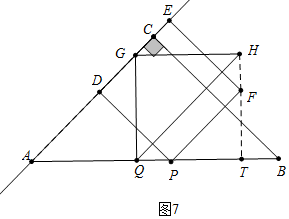
��TB=4-2��4-t��=4-$\frac{3}{2}$t�����t=$\frac{16}{7}$��
����ͼ8�У���HF��ABʱ����$\frac{1}{2}$t+t=4��
��t=$\frac{8}{3}$��
����������t=$\frac{8}{7}$s��$\frac{16}{7}$s��$\frac{8}{3}$ʱ��FH���ڵ�ֱ��ƽ�л�ֱ��AB��
���� ���⿼���ı����ۺ��⡢����ֱ�������ε����ʡ������ε����ʡ�ƽ�Ʊ任��֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ���ù������̵�˼��˼�����⣬ѧ���÷���������˼��˼�����⣬�����п�ѹ���⣮


 һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
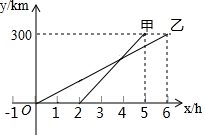 �ס����������ò�ͬ�Ľ�ͨ���ߣ���ͬһ·�ߴ�A�س���ǰ��B�أ��ҳ���2h����ٳ������Ҽס���������A�صľ���y����y����ʱ��x֮��ĺ���ͼ����ͼ��ʾ��
�ס����������ò�ͬ�Ľ�ͨ���ߣ���ͬһ·�ߴ�A�س���ǰ��B�أ��ҳ���2h����ٳ������Ҽס���������A�صľ���y����y����ʱ��x֮��ĺ���ͼ����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
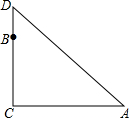 ��ͼ����һ����CD��10m�ߴ�B����ֻ���ӣ�����һֻ�����������ߵ�����20m���ij�����A������һֻ��������D��ֱ��Ծ��A����������ֱ���㣮�����ֻ�����������ľ�����ȣ�����������ж�ߣ�
��ͼ����һ����CD��10m�ߴ�B����ֻ���ӣ�����һֻ�����������ߵ�����20m���ij�����A������һֻ��������D��ֱ��Ծ��A����������ֱ���㣮�����ֻ�����������ľ�����ȣ�����������ж�ߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
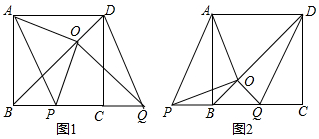
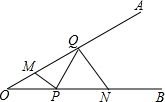 ��ͼ����AOB=30�㣬��M��N�ֱ��ڱ�OA��OB�ϣ�OM=$\sqrt{7}$��ON=3$\sqrt{2}$����P��Q�ֱ��ڱ�OB��OA���˶�������MP��PQ��QN����MP+PQ+QN����СֵΪ5��
��ͼ����AOB=30�㣬��M��N�ֱ��ڱ�OA��OB�ϣ�OM=$\sqrt{7}$��ON=3$\sqrt{2}$����P��Q�ֱ��ڱ�OB��OA���˶�������MP��PQ��QN����MP+PQ+QN����СֵΪ5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com