
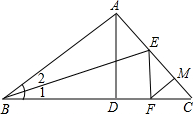
 如图,已知∠BAC=90°,AD⊥BC,∠1=∠2,EF⊥BC,FM⊥AC,说明FM=FD的理由.
如图,已知∠BAC=90°,AD⊥BC,∠1=∠2,EF⊥BC,FM⊥AC,说明FM=FD的理由.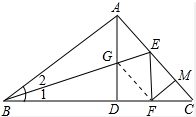 证明:如图所示:连接FG,
证明:如图所示:连接FG,
|


科目:初中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、y=(x-3)2+3 |
| B、y=(x-3)2+1 |
| C、y=(x-1)2+3 |
| D、y=(x-1)2+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,D是AB上的动点,E是BC上的动点,则AE+DE的最小值为( )
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,D是AB上的动点,E是BC上的动点,则AE+DE的最小值为( )A、3+2
| ||
| B、10 | ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源: 题型:
 四边形ABCD在平面直角坐标系中的位置,如图所示,已知A(-2,-3),B(2,-2),C(3,1),D(-1,0),求证:四边形ABCD是平行四边形.
四边形ABCD在平面直角坐标系中的位置,如图所示,已知A(-2,-3),B(2,-2),C(3,1),D(-1,0),求证:四边形ABCD是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:
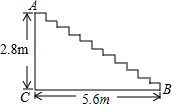 如图,某商场重新装修后,准备在大厅的主楼梯上铺设一种红色的地毯,已知这种地毯的价格为40元/m2,主楼梯的宽为3m,其侧面如图所示,则铺设这段楼梯至少需要多少元?
如图,某商场重新装修后,准备在大厅的主楼梯上铺设一种红色的地毯,已知这种地毯的价格为40元/m2,主楼梯的宽为3m,其侧面如图所示,则铺设这段楼梯至少需要多少元?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com