
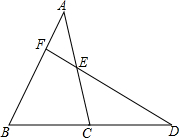
 在△ABC中,点D在BC的延长线上,E是AC边中点,DE的延长线交AB于点F.
在△ABC中,点D在BC的延长线上,E是AC边中点,DE的延长线交AB于点F.分析 (1)过C作CM∥AB交DF于M,求出DM=MF,证全等求出EF=ME,求出DM=MF=2EF,即可得出答案;
(2)由(1)知,CM=AF,根据CM∥BF,得到△CDM∽△BDF,于是得到$\frac{CM}{BF}=\frac{CD}{BD}$,根据已知条件$\frac{CD}{BC}=\frac{n}{m}$,得到$\frac{CD}{BD}$=$\frac{n}{m+n}$,即可得到结论.
解答 解:(1)过C作CM∥AB交DF于M,
∵CM∥BA,BC=CD,
∴DM=MF,
∵CM∥AB,
∴∠A=∠ECM,
∵E是AC的中点,
∴AE=EC,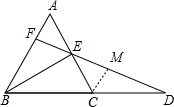
在△AFE和△CME中
$\left\{\begin{array}{l}{∠A=∠MCE}\\{AE=EC}\\{∠AEF=∠MEC}\end{array}\right.$,
∴△AFE≌△CME,
∴CM=AF,
∵CM∥BF,BC=CD,
∴CM=AF=$\frac{1}{2}$BF,
∴$\frac{AF}{BF}$=$\frac{1}{2}$;
(2)由(1)知,CM=AF,
∵CM∥BF,
∴△CDM∽△BDF,
∴$\frac{CM}{BF}=\frac{CD}{BD}$,
∵$\frac{CD}{BC}=\frac{n}{m}$,
∴$\frac{CD}{BD}$=$\frac{n}{m+n}$,
∴$\frac{AF}{BF}$=$\frac{CM}{BF}$=$\frac{CD}{BD}$=$\frac{n}{m+n}$.
点评 本题考查了全等三角形的判定和性质,平行线分线段成比例定理的应用,熟练掌握各定理是解题的关键.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某数学兴趣小组的同学再一次探究中发现:若平面直角坐标系中有两点A(x1,y1)和B(x2,y2),则线段AB的中点C的坐标为($\frac{{{x_1}+{x_2}}}{2},\frac{{{y_1}+{y_2}}}{2}$).经过进一步的讨论,他们呢借助中位线和一次函数的知识证明了这一结论,请你使用该结论解答下面问题.
某数学兴趣小组的同学再一次探究中发现:若平面直角坐标系中有两点A(x1,y1)和B(x2,y2),则线段AB的中点C的坐标为($\frac{{{x_1}+{x_2}}}{2},\frac{{{y_1}+{y_2}}}{2}$).经过进一步的讨论,他们呢借助中位线和一次函数的知识证明了这一结论,请你使用该结论解答下面问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
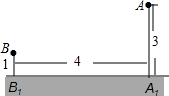 如图,大江的一侧有A、B两个工厂,它们有垂直于江边的小路,长度分别为3千米和1千米,设两条小路相距4千米,现在要在江边建立一个抽水站,把水送到A、B两厂去,欲使供水管路最短,抽水站应建在哪里?
如图,大江的一侧有A、B两个工厂,它们有垂直于江边的小路,长度分别为3千米和1千米,设两条小路相距4千米,现在要在江边建立一个抽水站,把水送到A、B两厂去,欲使供水管路最短,抽水站应建在哪里?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com