【答案】
分析:(1)由(
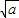
-
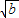
)
2≥0,利用完全平方公式,即可证得
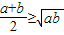
恒成立;
(2)由a
3+b
3+c
3-3abc=(a+b+c)(a
2+b
2+c
2-ab-bc-ac)=

(a+b+c)[(a-b)
2+(b-c)
2+(c-a)
2],可证得a
3+b
3+c
3≥3abc,即可得

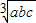
也恒成立;
(3)首先证得Rt△APC∽Rt△PBC,由相似三角形的对应边成比例,可求得PC的值,又由OP是半径,可求得OP=
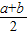
,然后由点到线的距离垂线段最短,即可证得

恒成立.
解答:解:(1)∵(
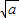
-
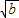
)
2≥0,
∴a-2
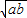
+b≥0,…(1分)
∴a+b≥2
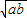
,…(2分)
∴
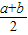
≥
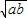
;…(3分)
(2)
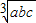
…(6分)
理由:a
3+b
3+c
3-3abc
=(a+b+c)(a
2+b
2+c
2-ab-bc-ac)
=

(a+b+c)(2a
2+2b
2+2c
2-2ab-2bc-2ac)
=

(a+b+c)[(a-b)
2+(b-c)
2+(c-a)
2]
∵a、b、c是正实数,
∴a
3+b
3+c
3-3abc≥0,
∴a
3+b
3+c
3≥3abc,
同理:
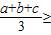
也恒成立;
故答案为:
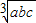
;
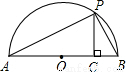
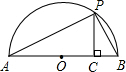
(3)如图,连接OP,
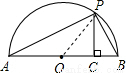
∵AB是直径,
∴∠APB=90°,
又∵PC⊥AB,
∴∠ACP=∠APB=90°,
∴∠A+∠B=∠A+∠APC=90°,
∴∠APC=∠B,
∴Rt△APC∽Rt△PBC,
∴
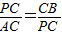
,
∴PC
2=AC•CB=ab,
∴PC=
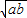
,…(7分)
又∵PO=
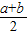
,
∵PO≥PC,
∴

.…(8分)
点评:此题考查了相似三角形的判定与性质、圆周角定理、几何不等式的应用与证明以及完全平方公式等知识.此题综合性较强,难度较大,注意数形结合思想的应用,注意完全平方式的非负性的应用.

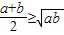 是恒成立的.
是恒成立的.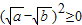 恒成立,说明
恒成立,说明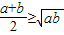 恒成立;
恒成立;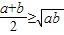 恒成立,猜测:
恒成立,猜测: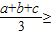 ______
______
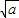 -
-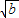 )2≥0,利用完全平方公式,即可证得
)2≥0,利用完全平方公式,即可证得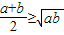 恒成立;
恒成立; (a+b+c)[(a-b)2+(b-c)2+(c-a)2],可证得a3+b3+c3≥3abc,即可得
(a+b+c)[(a-b)2+(b-c)2+(c-a)2],可证得a3+b3+c3≥3abc,即可得
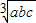 也恒成立;
也恒成立;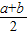 ,然后由点到线的距离垂线段最短,即可证得
,然后由点到线的距离垂线段最短,即可证得 恒成立.
恒成立.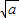 -
-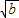 )2≥0,
)2≥0,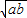 +b≥0,…(1分)
+b≥0,…(1分)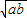 ,…(2分)
,…(2分)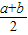 ≥
≥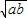 ;…(3分)
;…(3分)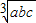 …(6分)
…(6分) (a+b+c)(2a2+2b2+2c2-2ab-2bc-2ac)
(a+b+c)(2a2+2b2+2c2-2ab-2bc-2ac)  (a+b+c)[(a-b)2+(b-c)2+(c-a)2]
(a+b+c)[(a-b)2+(b-c)2+(c-a)2]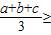
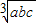 也恒成立;
也恒成立;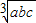 ;
;
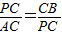 ,
,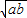 ,…(7分)
,…(7分)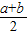 ,
, .…(8分)
.…(8分)

 (2012•资阳)已知a、b是正实数,那么,
(2012•资阳)已知a、b是正实数,那么, 已知a,b是正实数,
已知a,b是正实数,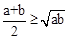 是恒成立的.
是恒成立的.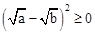 恒成立,说明
恒成立,说明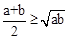 恒成立;
恒成立;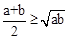 恒成立,猜测:
恒成立,猜测: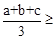 ▲ 也恒成立;
▲ 也恒成立;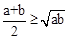 恒成立.
恒成立.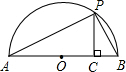
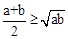 是恒成立的.
是恒成立的. 恒成立,说明
恒成立,说明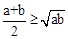 恒成立;
恒成立;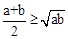 恒成立,猜测:
恒成立,猜测: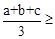 ▲ 也恒成立;
▲ 也恒成立;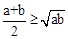 恒成立.
恒成立.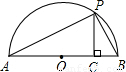
 已知a、b是正实数,那么,
已知a、b是正实数,那么, 是恒成立的.
是恒成立的.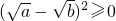 恒成立,说明
恒成立,说明 恒成立;
恒成立; 恒成立,猜测:
恒成立,猜测: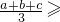 ______也恒成立;
______也恒成立; 恒成立.
恒成立.