练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．已知一列数：2，4，8，16，32…，我们发现，这一列数从第二项起，每一项与它前一项的比都等于2．
    一般地，如果一列数从第二项起，每一项与它前一项的比都等于同一个常数，这一列数就叫做等比数列，这个常数就叫做等比数列的公比．常用字母q表示．
    求：等比数列-3，9，-27，…的公比q=-3，第四项是81．

    分析 利用给出的方法和意义，计算每一项与它前一项的比，得出公比q，进一步计算得出第四项即可．

    解答 解：∵9÷（-3）=-3，
    -27÷9=-3，
    ∴等比数列-3，9，-27，…的公比q=-3，第四项是（-3）×（-3）×（-3）×（-3）=81．
    故答案为：-3，81．

    点评 此题考查数字的变化规律，理解题意，掌握等比数列的意义以及求公比和数列中每一项的计算方法是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    13．若a＜0，b＜0，则$\frac{|a|}{a}$+$\frac{|b|}{b}$=-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．按规律填空，并用字母表示一般规律：
    （1）2、4、6、8、10、12、14、…、2n
    （2）2、4、8、16、32、64、…、2n
    （3）1、3、7、13、21、31、…、n（n-1）+1
    （4）1、4、9、16、25、…、n2
    注：用n表示数的序号．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．将正整数依次按下表规律排成四列，则根据表中的排列规律，数2015应排的位置是第675行第3列
    第1列第2列第3列第4列
    第1行123
    第2行654
    第3行789
    第4行121110
    …

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．观察下面两个算式并回答问题：
    ①63×67=6×（6+1）×100+3×7=4200+21=4221；
    ②692×698=69×（69+1）×100+2×8=483000+16=483016．
    （1）两个因数个位上的数字之和是多少？其余各位上的数字有什么特征？
    （2）猜想符合上述特征的两数相乘的计算方法，并举例验证．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．已知一次函数y=kx+b的图象如图所示，则关于x的不等式k（x+2）+2b＞0的解集为x＞-8．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

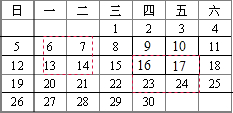    20．在日历上，我们可以发现其中某些数满足一定的规律．如图是2012年8月份的日历，我们任意选择其中所示的方框部分，将每个方框部分中4个位置上的数交叉相乘，再相减，例如：7×13-6×14=7，17×23-16×24=7．不难发现，结果都是7．
    （1）请你再选择两个类似的部分试一试．看看是否符合这个规律；
    （2）换一个月的日历试一下，是否有同样的规律？
    （3）请你利用整式的运算对以上的规律加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．请根据所给信息，帮助小樊同学完成他的调查报告
    调查目的了解八年级学生每天干家务活的平均时间
    调查内容秦淮区某中学八年级学生每天干家务活的平均时间
    调查方式抽样调查
    调查步骤 
    1、数据的收集：
    （1）在秦淮区某中学八年级每班随机调查5名学生；
    （2）统计这些学生2014年4月每天干家务活的平均时间（单位：min），
    结果如下（其中A表示10min；B表示20min；C表示30min）；
     
    BAABBBBACBBABBC
    ABAACABBCBABBAC
    2、数据的处理：
    以频数分布直方图的形式呈现上述统计结果，请补全频数分布直方图
     
    3、数据的分析
    列式计算所随机调查学生每天干家务活平均时间的平均数（结果保留整数）
     
    调查结论 
    秦淮区某中学八年级共有450名学生，其中大约有225名学生每天干家务活的平均时间是20min
    …

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．阅读下面的材料：
    高斯上小学时，有一次数学老师让同学们计算“从1到100这100个正整数的和”．许多同学都采用了依次累加的计算方法，计算起来非常烦琐，且易出错．聪明的小高斯经过探索后，给出了下面漂亮的解答过程．
    解：设S=1+2+3+…+100，①
    则S=100+99+98+…+1．②
    ①+②，得
    2S=101+101+101+…+101．
    （①②两式左右两端分别相加，左端等于2S，右端等于100个101的和）
    所以2S=100×101，
    S=（100×101）÷2  ③
    所以1+2+3+…+100=5 050．
    后来人们将小高斯的这种解答方法概括为“倒序相加法”．
    解答下面的问题：
    （1）请你运用高斯的“倒序相加法”计算：1+2+3+…+1000．
    （2）请你认真观察上面解答过程中的③式及你运算过程中出现类似的③式，猜想：1+2+3+…+n=$\frac{n（n+1）}{2}$．
    （3）请你利用（2）中你猜想的结论计算：1+2+3+…+2013．

    查看答案和解析>>

    同步练习册答案