
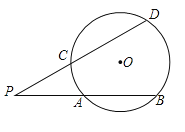
【题目】我们知道:顶点在圆上,并且两边都和圆相交的角叫做圆周角,一条弧所对的圆周角的度数等于它所对的圆心角度数的一半.类似地,我们定义:顶点在圆外,并且两边都和圆相交的角叫做圆外角.
(1)判断:图中有没有圆外角?如果有,请用字母表示出来.
(2)运用所学的数学知识,探究:圆外角的度数与它所夹的弧所对的圆心角的度数有什么关系?将你的发现,用文字表述出来,并说明理由.
科目:初中数学 来源: 题型:
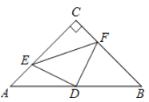
【题目】如图,在△ABC中,已知∠C=90°,AC=BC=4,D是AB的中点,点E,F分别在AC,BC上运动,(点E不与点A,C重合),且保持AE=CF,连接DE,EF,再次运动变化过程中,有下列结论:①四边形CEDF有可能成为正方形;②△DFE是等腰直角三角形;③四边形CEDF的面积是定值.其中正确的结论是:______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
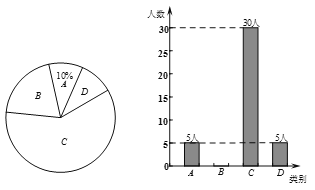
【题目】为了解阳光社区年龄20~60岁居民对垃圾分类的认识,学校课外实践小组随机抽取了该社区、该年龄段的部分居民进行了问卷调查,并将调查数据整理后绘成如下两幅不完整的统计图.图中A表示“全部能分类”,B表示“基本能分类”,C表示“略知一二”,D表示“完全不会”.请根据图中信息解答下列问题:
(1)补全条形统计图并填空:被调查的总人数是 人,扇形图中D部分所对应的圆心角的度数为 ;
(2)若该社区中年龄20~60岁的居民约3000人,请根据上述调查结果,估计该社区中C类有多少人?
(3)根据统计数据,结合生活实际,请你对社区垃圾分类工作提一条合理的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() 的直角顶点
的直角顶点![]() ,斜边
,斜边![]() 在
在![]() 轴上,且点
轴上,且点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 边上的一个动点,抛物线
边上的一个动点,抛物线![]() 过
过![]() ,
,![]() ,
,![]() 三点.
三点.
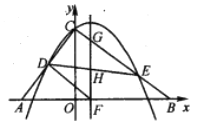
(1)当![]() 时,
时,
①求抛物线的解析式;
②平行于对称轴的直线![]() 与
与![]() 轴,
轴,![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() ,
,![]() ,若以点
,若以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的值.
的值.
(2)以![]() 为等腰三角形顶角顶点,
为等腰三角形顶角顶点,![]() 为腰构造等腰
为腰构造等腰![]() ,且
,且![]() 点落在
点落在![]() 轴上.若在
轴上.若在![]() 轴上满足条件的
轴上满足条件的![]() 点有且只有一个时,请直接写出点
点有且只有一个时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AC为直径的⊙O恰为△ABC的外接圆,∠ABC的平分线交⊙O于点D,过点D作DE∥AC交BC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AB=25,BC=![]() ,求DE的长.
,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCD的面积为20,顶点A在y轴上,顶点C在x轴上,顶点D在双曲线![]() 的图象上,边CD交y轴于点E,若
的图象上,边CD交y轴于点E,若![]() ,则k的值为______.
,则k的值为______.
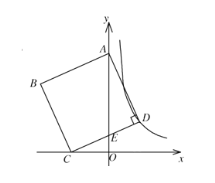
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过原点的直线与反比例函数![]() (k>0)的图象交于A,B两点,点A在第一象限点C在x轴正半轴上,连结AC交反比例函数图象于点D.AE为∠BAC的平分线,过点B作AE的垂线,垂足为E,连结DE.若AC=3DC,△ADE的面积为8,则k的值为____.
(k>0)的图象交于A,B两点,点A在第一象限点C在x轴正半轴上,连结AC交反比例函数图象于点D.AE为∠BAC的平分线,过点B作AE的垂线,垂足为E,连结DE.若AC=3DC,△ADE的面积为8,则k的值为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,在四边形ABCD中,AD//BC,∠C=90°动点P从点C出发沿线段CD向点D运动.到达点D即停止,若E、F分别是AP、BP的中点,设CP=x,△PEF的面积为y,且y与x之间的函数关系的图象如图乙所示,则线段AB长为( )
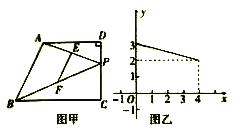
A.2![]() B.2
B.2![]() C.2
C.2![]() D.2
D.2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com