
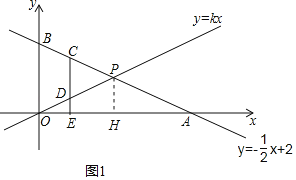
【题目】如图,在平面直角坐标系中,一次函数y=﹣![]() x+2的图象交x轴、y轴分别于点A,B,交直线y=kx于P.
x+2的图象交x轴、y轴分别于点A,B,交直线y=kx于P.
(1)求点A、B的坐标;
(2)若OP=PA,求P点坐标及k的值.
(3)在(2)的条件下,C是直线BP上一动点,CE⊥x轴于E,交直线DP于D,若CD=3ED,直接写出C点的坐标.

【答案】(1)点A的坐标为(4,0),点B的坐标为(0,2);(2)点P的坐标为(2,1),k=![]() ;(3)点C的坐标为(﹣4,4)或(
;(3)点C的坐标为(﹣4,4)或(![]() ,
,![]() ).
).
【解析】
(1)分别代入x=0、y=0求出y、x的值,由此可得出点B、A的坐标;
(2)作PH⊥OA于H,根据等腰三角形的性质可得出点P的坐标,再由点P在直线y=kx上求出k值;
(3)设点C的坐标为(m,﹣![]() m+2),得到点D的坐标为(m,
m+2),得到点D的坐标为(m,![]() m),得出CD、DE的长度,由题意得出关于m的一元一次方程,解方程得出结论.
m),得出CD、DE的长度,由题意得出关于m的一元一次方程,解方程得出结论.
解:(1)对于一次函数y=﹣![]() x+2,
x+2,
当y=0时,x=4,
当x=0时,y=2,
∴点A的坐标为(4,0),点B的坐标为(0,2);
(2)如图1,作PH⊥OA于H,
∵OP=AP,PH⊥OA,
∴OH=OA=![]() OA=2,
OA=2,
∴点P的横坐标为2,
∵点P在直线y=﹣![]() x+2上,
x+2上,
∴点P的纵坐标y=﹣![]() ×2+2=1,
×2+2=1,
∴点P的坐标为(2,1).
∵点P在直线y=kx上,
∴1=2k,解得:k=![]() ;
;
(3)设点C的坐标为(m,﹣![]() m+2),则点D的坐标为(m,
m+2),则点D的坐标为(m,![]() m),
m),
∴CD=|﹣![]() m+2﹣
m+2﹣![]() m|=|2﹣m|,DE=|
m|=|2﹣m|,DE=|![]() m|.
m|.
当m<0时,2﹣m=3×(﹣![]() m),
m),
解得,m=﹣4,
则点C的坐标为(﹣4,4);
当0<m<2时,2﹣m=3×![]() m,
m,
解得,m=![]() ,
,
则点C的坐标为(![]() ,
,![]() );
);
当2<m<4时,不存在点C;
当m>4时,m﹣2=3×![]() m,
m,
解得,m=﹣4(不合题意),
综上所述,CD=3ED时,点C的坐标为(﹣4,4)或(![]() ,
,![]() ).
).


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:①AF=AC;②DF=CF;③∠AFC=∠C;④∠BFD=∠CAF.
其中正确的结论个数有. ( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④![]() <a<
<a<![]() ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )

A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若△ABC的三边分别为a,b,c,其中a,b满足![]() +(b﹣8)2=0.
+(b﹣8)2=0.
(1)求边长c的取值范围,
(2)若△ABC是直角三角形,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款![]() 元,第三天收到捐款
元,第三天收到捐款![]() 元.
元.
![]() 如果第二天、第三天收到捐款的增长率相同,求捐款增长率?
如果第二天、第三天收到捐款的增长率相同,求捐款增长率?
![]() 按照
按照![]() 中收到捐款的增长率不变,该单位三天一共能收到多少捐款?
中收到捐款的增长率不变,该单位三天一共能收到多少捐款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是我国古代数学家杨辉最早发现的,称为“杨辉三角”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!

如图②是(a+b)n的三个展开式.结合上述两图之间的规律解题:
(1)请直接写出(a+b)4的展开式:(a+b)4= .
(2)请结合图②中的展开式计算下面的式:(x+2)3= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米.两车行驶的时间为x小时,y1、y2关于x的函数图象如图所示:

(1)根据图象,直接写出y1,y2关于x的函数关系式;
(2)当x为何值时,两车相遇?
(3)甲、乙两地间有A、B两个加油站,相距280千米,若客车进入A加油站时,出租车恰好进入B加油站,求A加油站离甲地的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com