
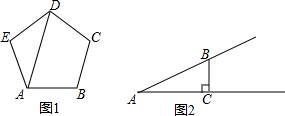
分析 A:用多边形内角和公式求得∠E的度数,在等腰三角形AED中可求得∠EAD的读数,进而求得∠BAD的度数;
B:通过后解直角三角形ABC来求AB的长度.
解答 解:A:∵正五边形ABCDE的内角和为(5-2)×180°=540°,
∴∠E=$\frac{1}{5}$×540°=108°,∠BAE=108°
又∵EA=ED,
∴∠EAD=$\frac{1}{2}$×(180°-108°)=36°,
∴∠BAD=∠BAE-∠EAD=72°.
故答案是:72°;
B:依题意得:AB=$\frac{AC}{cos27.5°}$=$\frac{10}{cos27.5°}$≈11.27.
故答案是:11.27.
点评 本题考查了解直角三角形的应用--坡度坡角问题.在解决坡度的有关问题中,一般通过作高构成直角三角形,坡角即是一锐角,坡度实际就是一锐角的正切值,水平宽度或铅直高度都是直角边,实质也是解直角三角形问题.应用领域:①测量领域;②航空领域 ③航海领域:④工程领域等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
 如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)正方形的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…,则顶点A2016的坐标为(504,-504).
如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)正方形的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…,则顶点A2016的坐标为(504,-504).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD为⊙O的内接四边形,且对角线AC为直径,AD=BC,过点D作DG⊥AC,垂足为E,DG分别与AB,⊙O及CB延长线交于点F、G、M.
如图,四边形ABCD为⊙O的内接四边形,且对角线AC为直径,AD=BC,过点D作DG⊥AC,垂足为E,DG分别与AB,⊙O及CB延长线交于点F、G、M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,两个完全一样的正方形ABOC和正方形DEMF,正方形DEMF的顶点E与正方形ABOC的中心重合,将正方形DEMF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.若AQ=12,BP=3,则PG=5.
如图所示,两个完全一样的正方形ABOC和正方形DEMF,正方形DEMF的顶点E与正方形ABOC的中心重合,将正方形DEMF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.若AQ=12,BP=3,则PG=5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com