下列命题中,是假命题的是( )
A.有一个内角等于60°的等腰三角形是等边三角形
B.在直角三角形中,斜边上的高等于斜边的一半
C.在直角三角形中,最大边的平方等于其他两边的平方和
D.三角形两个内角平分线的交点到三边的距离相等
【答案】
分析:A、根据等腰三角形的性质求解;B、根据直角三角形的面积计算方法求斜边的高;
C、根据勾股定理求解;D、求证角平分线和过角平分线交点作垂线所分的3对小三角形全等即可.
解答:解:A、等腰三角形底角相等,若底角为60°,则顶角为180°-60°-60°=60°,若顶角为60°,则底角为
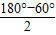
=60°,所以有一个角为60°的等腰三角形即为等边三角形,故A选项正确;
B、直角三角形中斜边的中线等于斜边的一半,只有在等腰直角三角形中斜边的高与斜边的中线才会重合,故B选项错误;
C、在直角三角形中,最大的边为斜边,根据勾股定理可知斜边长的平方的等于两直角边长平方的和,故C选项正确;
D、过三角形角平分线的交点作各边的垂线,则三角形分成3对小三角形,其中各顶点所在的两个直角三角形全等,即过角平分线作的高线相等,故D选项正确;
即B选项中命题为假命题,
故选 B.
点评:本题考查了全等三角形的证明,考查了直角三角形中勾股定理的运用,考查了等腰三角形的性质,考查了直角三角形中斜边上的中线等于斜边长一半的性质.

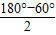 =60°,所以有一个角为60°的等腰三角形即为等边三角形,故A选项正确;
=60°,所以有一个角为60°的等腰三角形即为等边三角形,故A选项正确;

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案