
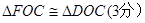
 的值(3分)
的值(3分)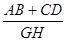 的值(3分)
的值(3分)
 AB,
AB, AB,
AB,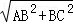 =
=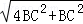 =
=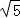 BC,
BC,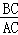 =
=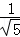 =
=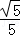 ;(3分)
;(3分)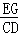 =
= =
= ,即EG=
,即EG= CD,
CD, CD,
CD,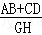 =
=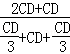 =
=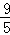 .(3分)
.(3分)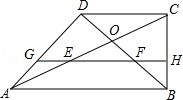
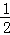 AB,又CD∥AB,CD=
AB,又CD∥AB,CD=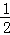 AB,可得EF=CD,由平行线的性质可证△FOE≌△DOC;
AB,可得EF=CD,由平行线的性质可证△FOE≌△DOC;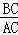 ,由勾股定理得出AC与BC的关系,再求正弦值;
,由勾股定理得出AC与BC的关系,再求正弦值;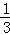 CD,同理得FH=
CD,同理得FH=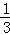 CD,又AB=2CD,代入
CD,又AB=2CD,代入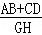 中求值.
中求值.

科目:初中数学 来源:不详 题型:解答题
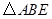 沿
沿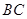 方向平移,使点E与点C重合,得
方向平移,使点E与点C重合,得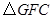 .
.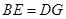 ;
;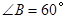 ,当AB与BC满足什么数量关系时,四边形
,当AB与BC满足什么数量关系时,四边形 是菱形?证明你的结论.
是菱形?证明你的结论.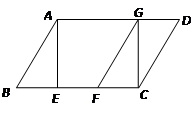
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
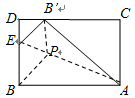
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
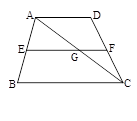
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
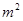 ,
,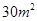 ,
,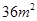 ,则种植白色花卉土地的面积为 m2.
,则种植白色花卉土地的面积为 m2.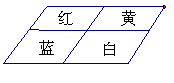
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com