
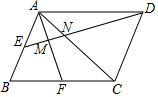
 如图,点E,F分别是?ABCD两边AB、BC的中点,且AF、AC分别与ED交于M、N两点,有下列结论:①MN:ME=2:3;②MN:DN=1:4;③N是DE的三等分点;④△AMN~△DMA.其中正确的是:①③.(把所有正确结论的序号都选上)
如图,点E,F分别是?ABCD两边AB、BC的中点,且AF、AC分别与ED交于M、N两点,有下列结论:①MN:ME=2:3;②MN:DN=1:4;③N是DE的三等分点;④△AMN~△DMA.其中正确的是:①③.(把所有正确结论的序号都选上) 分析 如图1中,延长DC交AF于H.与△ABF≌△CHF,推出AB=CF=CD,由AE=EB,AE∥DH,推出$\frac{EM}{MD}$=$\frac{AE}{DH}$=$\frac{1}{4}$,$\frac{EN}{DN}$=$\frac{AE}{CD}$=$\frac{1}{2}$,设EM=a,则DM=4a,EN=$\frac{5}{3}$a,DN=$\frac{10}{3}$a,MN=$\frac{2}{3}$a,可得EM:MN=3:2,MN:DN=1:5,EN:DN=1:2,推出①③正确,②错误,如图2中,当AF⊥BC时,显然⊥ANM≠∠MAD,∴△AMN与△ADM不相似.故④错误.
解答 解:如图1中,延长DC交AF于H.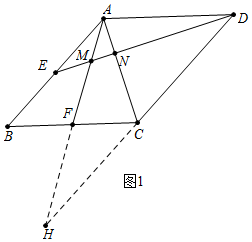
∵四边形ABCD是平行四边形,
∴AB∥DH,AB=CD,
∴∠B=∠HCF,
在△ABF和△HCF中,
$\left\{\begin{array}{l}{∠B=∠HCF}\\{FB=CF}\\{∠ABF=∠CFH}\end{array}\right.$,
∴△ABF≌△CHF,
∴AB=CF=CD,
∵AE=EB,AE∥DH,
∴$\frac{EM}{MD}$=$\frac{AE}{DH}$=$\frac{1}{4}$,$\frac{EN}{DN}$=$\frac{AE}{CD}$=$\frac{1}{2}$,设EM=a,则DM=4a,EN=$\frac{5}{3}$a,DN=$\frac{10}{3}$a,MN=$\frac{2}{3}$a,
∴EM:MN=3:2,MN:DN=1:5,EN:DN=1:2,
∴①③正确,②错误,
如图2中,当AF⊥BC时,显然⊥ANM≠∠MAD,∴△AMN与△ADM不相似.故④错误.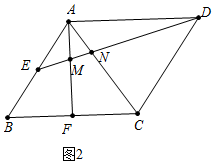
故答案为①③.
点评 本题考查相似三角形的判定和性质、平行线的性质等知识,解题的关键是学会添加辅助线,构造相似三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
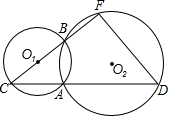 如图,已知⊙O1与⊙O2交于A,B两点,点C在⊙O1上且在⊙O2外,CA,CB的延长线分别与⊙O2交于点D,E,AC=3,AD=6,⊙O1的半径为2.则点O1到DE的距离为 ( )
如图,已知⊙O1与⊙O2交于A,B两点,点C在⊙O1上且在⊙O2外,CA,CB的延长线分别与⊙O2交于点D,E,AC=3,AD=6,⊙O1的半径为2.则点O1到DE的距离为 ( )| A. | $\frac{17}{4}$ | B. | $\frac{9}{2}$ | C. | $\frac{19}{4}$ | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
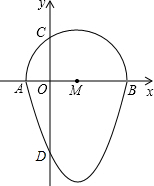 如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2-2x-3,求这个“果圆”被y轴截得线段CD的长3+$\sqrt{3}$.
如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2-2x-3,求这个“果圆”被y轴截得线段CD的长3+$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
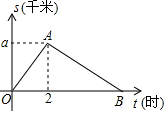 某单位举行“健康人生”徒步走活动,某人从起点体育村沿建设路到市生态园,再沿原路返回,设此人离开起点的路程s(千米)与走步时间t(小时)之间的函数关系如图所示,其中从起点到市生态园的平均速度是4千米/小时,用2小时,根据图象提供信息,解答下列问题.
某单位举行“健康人生”徒步走活动,某人从起点体育村沿建设路到市生态园,再沿原路返回,设此人离开起点的路程s(千米)与走步时间t(小时)之间的函数关系如图所示,其中从起点到市生态园的平均速度是4千米/小时,用2小时,根据图象提供信息,解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com