
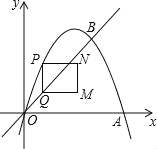
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx与x轴交于O、A两点,与直线y=x交于点B,点A、B的坐标分别为(3,0)、(2,2).点P在抛物线上,过点P作y轴的平行线交射线OB于点Q,以PQ为边向右作矩形PQMN,且PN=1,设点P的横坐标为m(m>0,且m≠2).
(1)求这条抛物线所对应的函数表达式.
(2)求矩形PQMN的周长C与m之间的函数关系式.
(3)当矩形PQMN是正方形时,求m的值.
【答案】(1)y=﹣x2+3x.(2)①当0<m<2时,C=﹣2m2+4m+2.②当m>2时,C=2m2﹣4m+2.(3)1或1+![]() .
.
【解析】
试题分析: (1)把A(3,0)、B(2,2)两点坐标代入y=ax2+bx,解方程组即可解决.
(2)分两种情形:①0<m<2,②m>2,分别求出矩形PQMN的周长C与m之间的函数关系式即可.
(3)分两种情形列出方程即可解决.
试题解析:(1)把A(3,0)、B(2,2)两点坐标代入y=ax2+bx,
得![]() ,解得
,解得![]() .
.
故抛物线所对应的函数表达式为y=﹣x2+3x.
(2)∵点P在抛物线y=﹣x2+3x上,
∴可以设P(m,﹣m2+3m),
∵PQ∥y轴,
∴Q(m,m).
①当0<m<2时,如图1中,

PQ=﹣m2+3m﹣m=﹣m2﹣2m,
C=2(﹣m2+2m)+2=﹣2m2+4m+2.
②当m>2时,如图2中,

PQ=m﹣(﹣m2+3m)=m2﹣2m,
C=2(m2﹣2m)+2=2m2﹣4m+2.
(3)∵矩形PQMN是正方形,
∴PQ=PN=1,
当0<m<2时,如图3中,

﹣m2+2m=1,解得m=1.
当m>2时,如图4中,

m2﹣2m=1,解得m=1+![]() (或1﹣
(或1﹣![]() 不合题意舍弃).
不合题意舍弃).


科目:初中数学 来源: 题型:
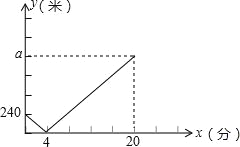
【题目】小明家、学校与图书馆依次在一条直线上,小明、小亮两人同时分别从小明家和学校出发沿直线匀速步行到图书馆借阅图书,小明到达图书馆花了20分钟,小亮每分钟步行40米,小明离学校的距离y(米)与两人出发时间x(分)之间的函数图象如图所示.
(1)小明每分钟步行 米,a= ,小明家离图书馆的距离为 米.
(2)在图中画出小亮离学校的距离y(米)与x(分)之间的函数图象.
(3)求小明和小亮在途中相遇时二人离图书馆的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
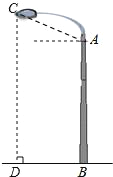
【题目】如图,某广场有一灯柱AB高7.5米,灯的顶端C离灯柱顶端A的距离CA为1.7米,且∠CAB=110°,求灯的顶端C距离地面的高度CD.(结果精确到0.1米)
【参考数据:sin20°=0.34,cos20°=0.94,tan20°=0.36】
查看答案和解析>>
科目:初中数学 来源: 题型:
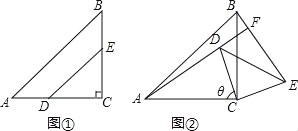
【题目】如图①,在△ABC中,∠ACB=90°,AC=BC,在AC、BC边上分别截取CD=CE,连结DE.将△DCE绕着点C顺时针旋转θ角,连结BE、AD.
(1)当0°<θ<90°时,如图②,直线BE交直线AD于点F.
①求证:△ACD≌△BCE.
②求证:AF⊥BE.
(2)当0°<θ<360°,AC=5,CD=3,四边形CDFE是正方形时,直接写出AF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】种一批树苗,如果每人种10棵,则剩6棵树苗未种,如果每人种12棵,则缺14棵树苗.问有多少人参加种树?设有x人参加种树,可列出方程 ______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形的一边长为3 cm,周长为19 cm,则该三角形的腰长为 ( )
A. 3 cmB. 8 cmC. 3 cm或8 cmD. 以上答案均不对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com