
【题目】把抛物线y=﹣x2向右平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为 .
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知∠A是钝角,∠A与∠B互补,∠B与∠C互余,则∠A与∠C的关系式为( )
A. ∠A -∠C=90° B. ∠A +∠C=90° C. ∠A +∠C=180° D. ∠A =∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线![]() :
:![]() 与
与![]() :
:![]() 为“友好抛物线”.
为“友好抛物线”.
(1)求抛物线![]() 的解析式.
的解析式.
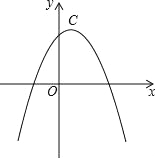
(2)点A是抛物线![]() 上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.
上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.
(3)设抛物线![]() 的顶点为C,点B的坐标为(﹣1,4),问在
的顶点为C,点B的坐标为(﹣1,4),问在![]() 的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线
的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线![]() 上?若存在求出点M的坐标,不存在说明理由.
上?若存在求出点M的坐标,不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是点是【A,B】的好点.
(1)如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点; 又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D【A,B】的好点,但点D【B,A】的好点.(请在横线上填是或不是)知识运用: 
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2.数所表示的点是【M,N】的好点; 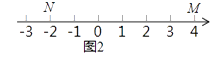
(3)如图3,A、B为数轴上两点,点A所表示的数为﹣20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以4个单位每秒的速度向左运动,到达点A停止.当经过秒时,P、A和B中恰有一个点为其余两点的好点? 
查看答案和解析>>
科目:初中数学 来源: 题型:
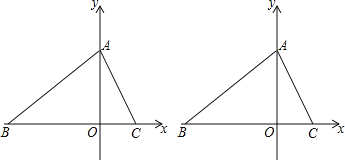
【题目】如图,在平面直角坐标系中,O为坐标原点.三角形ABC的边BC在石轴上,点B的坐标是(-5,0),点A在y轴的正半轴上,点C在x轴的正半轴上,它们的坐标分别为A(0,m)、C(m-1,0),且OA+OC=7,动点P从点B出发,以每秒2个单位的速度,沿射线BO运动.设点P运动时间为t秒.
(1)求A、C两点的坐标;
(2)连结PA,当P沿射线BO匀速运动时,是否存在某一时刻,使三角形POA的面积是三角形ABC面积的![]() ?若存在,请求出t的值,并写出P点坐标;若不存在,请说明理由.
?若存在,请求出t的值,并写出P点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com