
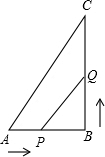
 如图所示,△ABC中,AB=6厘米,BC=8厘米,∠B=90°,AB=6厘米,BC=8厘米,点P从点A开始沿AB边向B以1厘米/秒的速度移动,点Q从B点开始沿BC边向点C以2厘米/秒的速度移动.
如图所示,△ABC中,AB=6厘米,BC=8厘米,∠B=90°,AB=6厘米,BC=8厘米,点P从点A开始沿AB边向B以1厘米/秒的速度移动,点Q从B点开始沿BC边向点C以2厘米/秒的速度移动.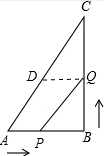 解:(1)设经过x秒使△PBQ得面积等于8平方厘米,根据题意得:
解:(1)设经过x秒使△PBQ得面积等于8平方厘米,根据题意得:| 1 |
| 2 |
| QD |
| 2x-8 |
| AB |
| AC |
| 6(2x-8) |
| 10 |
| 1 |
| 2 |
| 6(2x-8) |
| 10 |


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com