
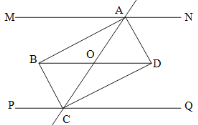
【题目】如图所示,已知直线MN//PQ,直线AC交MN、PQ于点A、C,所得的同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.试猜想AC与BD的关系,并说明理由.
【答案】AC与BD相等且互相平分,理由见解析.
【解析】
已知MN//PQ,可得∠MAC+∠ACP=180°,已知AB、CB分别平分∠MAC、∠ACP,即∠BAC=![]() ∠MAC,∠BCA=
∠MAC,∠BCA=![]() ∠ACP,得到∠BAC+∠BCA=90°,∠ABC=90°,同理可得∠ADC=90°,根据角平分线的性质可得到∠ACB+∠ACD=90°,即∠BCD=90°,证得四边形ABCD是矩形,得到AC与BD相等且互相平分.
∠ACP,得到∠BAC+∠BCA=90°,∠ABC=90°,同理可得∠ADC=90°,根据角平分线的性质可得到∠ACB+∠ACD=90°,即∠BCD=90°,证得四边形ABCD是矩形,得到AC与BD相等且互相平分.
AC与BD相等且互相平分,理由如下:
∵MN//PQ,
∴ ∠MAC+∠ACP=180°
又∵AB、CB分别平分∠MAC、∠ACP
∴∠BAC=![]() ∠MAC,∠BCA=
∠MAC,∠BCA=![]() ∠ACP
∠ACP
∴∠BAC+∠BCA=90°
∴∠ABC=90°
同理可得∠ADC=90°
又∠ACP+∠ACQ=180°,CB、CD分别平分∠ACP、∠ACQ
∴∠ACB+∠ACD=90°
即∠BCD=90°
∴四边形ABCD是矩形
∴AC与BD相等且互相平分


科目:初中数学 来源: 题型:
【题目】如图,在一块正方形ABCD木板上要贴三种不同的墙纸,正方形EFCG部分贴A型墙纸,△ABE部分贴B型墙纸,其余部分贴C型墙纸.A型、B型、C型三种墙纸的单价分别为每平方米60元、80元、40元.
探究1:如果木板边长为1米,FC=![]() 米,则一块木板用墙纸的费用需 元;
米,则一块木板用墙纸的费用需 元;
探究2:如果木板边长为2米,正方形EFCG的边长为x米,一块木板需用墙纸的费用为y元,

(1)用含x的代数式表示y(写过程).
(2)如果一块木板需用墙纸的费用为225元,求正方形EFCG的边长为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() (x+1)(x﹣3)与x轴交于A、B两点,与y轴交于点C,点D为该抛物线的对称轴上一点,当点D到直线BC和到x轴的距离相等时,则点D的坐标为 .
(x+1)(x﹣3)与x轴交于A、B两点,与y轴交于点C,点D为该抛物线的对称轴上一点,当点D到直线BC和到x轴的距离相等时,则点D的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
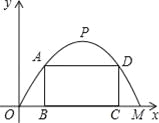
【题目】施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米,现在O点为原点,OM所在直线为x轴建立直角坐标系(如图所示).
(1)直接写出点M及抛物线顶点P的坐标;
(2)求出这条抛物线的函数解析式;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABCD,使A、D点在抛物线上,B、C点在地面OM上.为了筹备材料,需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少?请你帮施工队计算一下.
查看答案和解析>>
科目:初中数学 来源: 题型:
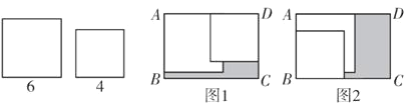
【题目】如图,已知在矩形ABCD内,将两张边长分别为6和4的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中末被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.当AD-AB=2时,S2-S1的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:
A型 | B型 | |
价格(万元/台) | 12 | 10 |
月污水处理能力(吨/月) | 200 | 160 |
经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.
(1)该企业有几种购买方案?
(2)哪种方案更省钱,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22019的值.
解:设S=1+2+22+23+24+…+22019,将等式两边同时乘以2得:2S=2+22+23+24+25+…+22019+22020
将下式减去上式得2S-S=22020-1
即S=22020-1
即1+2+22+23+24+…=22020-1
请你仿照此法计算:
(1)1+2+22+23+24+…+220
(2)1+5+52+53+54+…+5n(其中n为正整数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com