
 如图,⊙O半径为3,Rt△ABC的顶点A,B在⊙O上,∠A=30°,点C在⊙O内,当点A在圆上运动时,OC的最小值为( )
如图,⊙O半径为3,Rt△ABC的顶点A,B在⊙O上,∠A=30°,点C在⊙O内,当点A在圆上运动时,OC的最小值为( )| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 连接AO,当OC⊥OA时,OC最短,由∠B=90°,得到BC延长线与AO的延长线交于D,点D会在圆上,得到AC=CD,解直角三角形得到CD=AC=2CB,AB=$\sqrt{3}$BC,根据勾股定理即可得到结论.
解答 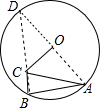 解:连接AO,当OC⊥OA时,OC最短,
解:连接AO,当OC⊥OA时,OC最短,
∵∠B=90°,
∴BC延长线与AO的延长线交于D,点D会在圆上,
∵OC⊥AD,OA=OD,
∴AC=CD,
∵∠CAB=30°,
∴CD=AC=2CB,AB=$\sqrt{3}$BC,
∵AD2=BD2+AB2=9BC2+3BC2,
∴BC=$\sqrt{3}$,
∴AC=2$\sqrt{3}$,
∵AO=3,
∴OC=$\sqrt{3}$.
故选C.
点评 本题考查了圆周角定理,垂线段最短,勾股定理,正确作出辅助线是解题的关键.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
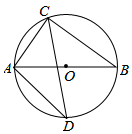 如图,AB是⊙O的直径,弦AC=6,BC=8,弦CD平分∠ACB.
如图,AB是⊙O的直径,弦AC=6,BC=8,弦CD平分∠ACB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
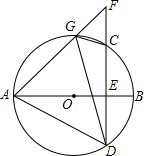 如图,AB是⊙O直径,弦CD⊥AB于点E,G是弧AC上任意一点,延长AG,与DC的延长线相交于点F,连结AD,GD,CG,则与∠AGD相等的角有( )
如图,AB是⊙O直径,弦CD⊥AB于点E,G是弧AC上任意一点,延长AG,与DC的延长线相交于点F,连结AD,GD,CG,则与∠AGD相等的角有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 a,b,c大小关系如图,下列各式①b+a+(-c)>0;②(-a)-b+c>0;③$\frac{a}{|a|}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1;④bc-a>0;⑤|a-b|-|c+b|+|a-c|=-2b,其中正确的有( )
a,b,c大小关系如图,下列各式①b+a+(-c)>0;②(-a)-b+c>0;③$\frac{a}{|a|}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1;④bc-a>0;⑤|a-b|-|c+b|+|a-c|=-2b,其中正确的有( )| A. | ②⑤ | B. | ②③ | C. | ②③⑤ | D. | ②③④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
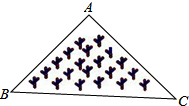 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪的三个顶点的距离相等,凉亭的位置应选在( )
如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪的三个顶点的距离相等,凉亭的位置应选在( )| A. | △ABC三边的垂直平分线的交点 | B. | △ABC的三条中线的交点 | ||
| C. | △ABC三条角平分线的交点 | D. | △ABC三条高所在直线的交点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com