
 某地区教育部门为了了解本地九年级学生每周“阳光体育活动”的时间情况,随机调査了本地部分九年级学生,把收集到的数据进行整理并制成了以下两幅统汁图.学生“阳光体育活动”的时间x(h)分为五个等级:A(x≤4),B(4<x≤6),C(6<x≤8),D(8<x≤l0>,E(x>10).
某地区教育部门为了了解本地九年级学生每周“阳光体育活动”的时间情况,随机调査了本地部分九年级学生,把收集到的数据进行整理并制成了以下两幅统汁图.学生“阳光体育活动”的时间x(h)分为五个等级:A(x≤4),B(4<x≤6),C(6<x≤8),D(8<x≤l0>,E(x>10).分析 (1)由统计图可知A等级占5%,有10个人,从而可以得到本次共调查的学生数;
(2)根据扇形统计图可以求得m的值,也可以求出D等级的学生数,从而可以将条形统计图补充完整;
(3)根据加权平均数的计算方法可以解答本题;
(4)根据统计图中的数据可以解答本题.
解答  解:(1)由题意可得,
解:(1)由题意可得,
10÷5%=200,
即本次共调查了200名学生;
(2)m%=1-45%-12%-5%-8%=30%,
故答案为:30;
D等级的学生数为:200×30%=60,
补全的条形统计图如右图所示,
(3)被调查学生平均每周的活动时间为:$\frac{3×10+5×200×12%+7×90+9×60+11×200×8%}{200}$=7.48h,
即被调查学生平均每周的活动时间是7.48h;
(4)8000×(45%+30%+8%)=6640(名),
即每周“阳光体育活动”时间大于6h的学生有6640名.
点评 本题考查条形统计图、扇形统计图、用样本估计总体、加权平均数,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
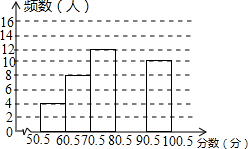 2015年11月9日是第25个全国消防日,某学校为了增强学生的安全意识,举行了一次安全知识竞赛,全校800名学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中随机抽取了部分学生的成绩进行统计(满分100分,而且成绩均为整数).绘制了不完整的统计图表,请你根据图表中提供的信息解答以下问题:
2015年11月9日是第25个全国消防日,某学校为了增强学生的安全意识,举行了一次安全知识竞赛,全校800名学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中随机抽取了部分学生的成绩进行统计(满分100分,而且成绩均为整数).绘制了不完整的统计图表,请你根据图表中提供的信息解答以下问题:| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | 12 | m |
| 80.5~90.5 | n | 0.32 |
| 90.5~100.5 | 10 | 0.1 |
| 合计 | a | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A、B为x轴上的两点,点C、D为y轴上的两点,经过A、C、B的抛物线C1的一部分与经过点A、D、B的抛物线C2的一部分组合成一条封闭曲线,我们把这条封闭曲线成为“月线”.已知点C的坐标为(0,3),点M是抛物线C2:y=mx2-4mx-12m(m<0)的顶点.
如图,点A、B为x轴上的两点,点C、D为y轴上的两点,经过A、C、B的抛物线C1的一部分与经过点A、D、B的抛物线C2的一部分组合成一条封闭曲线,我们把这条封闭曲线成为“月线”.已知点C的坐标为(0,3),点M是抛物线C2:y=mx2-4mx-12m(m<0)的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | -1 | C. | 1 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com