
【题目】如图示,三角形ABC是等边三角形,D是BC边上的一点,三角形ABD经过旋转后到达三角形ACE的位置.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后,点M到了什么位置?

【答案】(1)点A;(2)60°;(3)点M到了AC的中点处.
【解析】(1)观察图形,由于△ABC是等边三角形,D是BC上一点,△ABD经旋转后到达△ACE的位置,可得出旋转中心;
(2)观察图形,线段AB旋转后,对应边是AC,∠BAC就是旋转角,可得出旋转角;
(3)因为旋转前后AB、AC是对应边,故AB的中点M,旋转后就是AC的中点了.
(1)∵△ABD经旋转后到达△ACE,它们的公共顶点为A,
∴旋转中心是点A;
(2)线段AB旋转后,对应边是AC,∠BAC就是旋转角,也是等边三角形的内角,是60°,
∴旋转了60°;
(3)∵旋转前后AB,AC是对应边,故AB的中点M,旋转后就是AC的中点了,
∴点M转到了AC的中点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(1)观察思考
如图所示,线段AB上的点数与线段的总条数有如下关系:如果线段AB上有3个点,那么线段总条数为3;如果线段AB上有4个点,那么线段总条数为6;如果线段AB上有5个点,那么线段总条数为________.
![]() 3=2+1=
3=2+1=![]()
![]() 6=3+2+1=
6=3+2+1=![]()
![]()
(2)模型构建
如果线段上有m个点(包括线段的两个端点),那么共有________条线段.
(3)拓展应用
8位同学参加班上组织的象棋比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),那么一共要进行多少场比赛?
请将这个问题转化为上述模型,并直接应用上述模型的结论解决问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,
∠BAD=45°,AD与BE交于点F,连接CF.
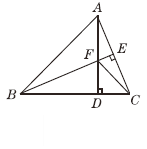
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分类
﹣3,0.45, ![]() ,0,9,﹣1,﹣1
,0,9,﹣1,﹣1![]() ,10,﹣3.14
,10,﹣3.14
(1)正整数:{ …}
(2)负整数:{ …}
(3)整数:{ …}
(4)分数:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线C1:y=a(x+1)(x﹣3a)(a>0)与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,﹣3)
(1)求抛物线C1的解析式及A,B点坐标;
(2)求抛物线C1的顶点坐标;
(3)将抛物线C1向上平移3个单位长度,再向左平移n(n>0)个单位长度,得到抛物线C2 , 若抛物线C2的顶点在△ABC内,求n的取值范围. (在所给坐标系中画出草图C1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中, ①AE和BF的位置关系为;
②线段MN的最小值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果∠A和∠B互补,且∠A>∠B,给出下列四个式子:①90°﹣∠B;②∠A﹣90°;③![]() (∠A+∠B)④
(∠A+∠B)④![]() (∠A﹣∠B)其中表示∠B余角的式子有_____.(填序号)
(∠A﹣∠B)其中表示∠B余角的式子有_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.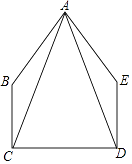
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com