探究问题
(1)方法感悟:
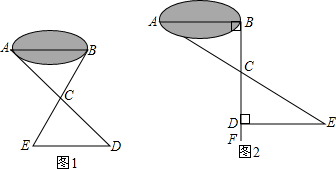
一班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:
方案(Ⅰ)如图1,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长;感悟解题方法,并完成下列填空:
解:在如图所示的两个三角形△DEC和△ABC中:DC=AC,∠
ACB
ACB
=∠
DCE
DCE
(对顶角相等),EC=BC,∴△DEC≌△ABC
(SAS)
(SAS)
,∴DE=AB(全等三角形对应边相等),即DE的距离即为AB的长.
(2)方法迁移:
方案(Ⅱ)如图2,先过B点作AB的垂线BF,再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.请你说明理由.
(3)问题拓展:
方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是
作∠ABC=∠EDC=90°
作∠ABC=∠EDC=90°
;若仅满足∠ABD=∠BDE≠90°,方案(Ⅱ)是否成立?
成立
成立
.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
