
【题目】如图,在平面直角坐标系xOy中,点A(3,3),点B(4,0),点C(0,﹣1).
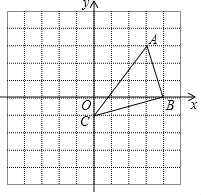
(1)以点C为中心,把△ABC逆时针旋转90°,请在图中画出旋转后的图形△A′B′C,点B′的坐标为________;
(2)在(1)的条件下,求出点A经过的路径![]() 的长(结果保留π).
的长(结果保留π).
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的图象如图所示:
的图象如图所示:
(1)将该抛物线向上平移2个单位,分别交x轴于A、B两点,交y轴于点C,则平移后的解析式为 .
(2)判断△ABC的形状,并说明理由.
(3)在抛物线对称轴上是否存在一点P,使得以A、C、P为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣x+3与x轴、y轴分别交于点B、C;抛物线y=﹣x2+bx+c经过B、C两点,并与x轴交于另一点A.
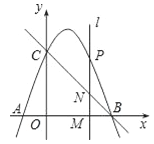
(1)求该抛物线所对应的函数关系式;
(2)设P(x,y)是(1)所得抛物线上的一个动点,过点P作直线l⊥x轴于点M,交直线BC于点N.
①若点P在第一象限内.试问:线段PN的长度是否存在最大值?若存在,求出它的最大值及此时x的值;若不存在,请说明理由;
②求以BC为底边的等腰△BPC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于_____.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923101670465536/1923902127538176/STEM/3534c7f6f1a5489684ae6308493b71da.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,直径DE⊥AB于点F,交BC于点 M,DE的延长线与AC的延长线交于点N,连接AM.

(1)求证:AM=BM;
(2)若AM⊥BM,DE=8,∠N=15°,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为1,点M是BC边上的动点(不与B,C重合),点N是AM的中点,过点N作EF⊥AM,分别交AB,BD,CD于点E,K,F,设BM=x.
(1)AE的长为______(用含x的代数式表示);
(2)设EK=2KF,则![]() 的值为______.
的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数![]() 的图象分别交于点B1、B2、B3,分别过点B1、B2、B3作x轴的平行线,分别与y轴交于点C1、C2、C3,连结OB1、OB2、OB3,那么图中阴影部分的面积之和为 .
的图象分别交于点B1、B2、B3,分别过点B1、B2、B3作x轴的平行线,分别与y轴交于点C1、C2、C3,连结OB1、OB2、OB3,那么图中阴影部分的面积之和为 .
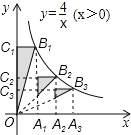
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D.
(1)在图(1)中,用直尺和圆规过点D作⊙O的切线DE交BC于点E;(保留作图痕迹,不写作法)
(2)如图(2),如果⊙O的半径为3,ED=4,延长EO交⊙O于F,连接DF,与OA交于点G,求OG的长.
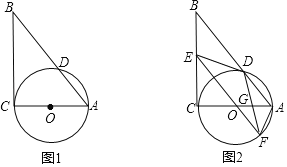
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com