
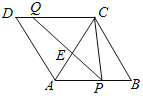
【题目】如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点为A′,当CA′的长度最小时,CQ的长为_____.
【答案】7
【解析】
作CH⊥AB于H,如图,根据菱形的性质可判断△ABC为等边三角形,则CH=![]() AB=4
AB=4![]() ,AH=BH=4,再利用勾股定理计算出CP=7,再根据折叠的性质得点A′在以P点为圆心,PA为半径的弧上,利用点与圆的位置关系得到当点A′在PC上时,CA′的值最小,然后证明CQ=CP即可.
,AH=BH=4,再利用勾股定理计算出CP=7,再根据折叠的性质得点A′在以P点为圆心,PA为半径的弧上,利用点与圆的位置关系得到当点A′在PC上时,CA′的值最小,然后证明CQ=CP即可.
作CH⊥AB于H,如图,
∵菱形ABCD的边AB=8,∠B=60°,
∴△ABC为等边三角形,
∴CH=![]() AB=4
AB=4![]() ,AH=BH=4,
,AH=BH=4,
∵PB=3,
∴HP=1,
在Rt△CHP中,CP=![]() =7,
=7,
∵梯形APQD沿直线PQ折叠,A的对应点A′,
∴点A′在以P点为圆心,PA为半径的弧上,
∴当点A′在PC上时,CA′的值最小,
∴∠APQ=∠CPQ,而CD∥AB,
∴∠APQ=∠CQP,
∴∠CQP=∠CPQ,
∴CQ=CP=7.
故答案为:7.



 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
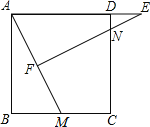
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+bx+c交x轴于点A(- 4,0)和点B,交y轴于点C(0,4).
(1)求抛物线的函数表达式;
(2)如图2,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,当△ADC面积有最大值时,在抛物线对称轴上找一点M,使DM+AM的值最小,求出此时M的坐标;
(3)点Q在直线AC上的运动过程中,是否存在点Q,使△BQC为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
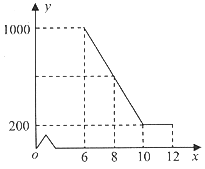
【题目】某驻村扶贫小组实施产业扶贫,帮助贫困农户进行西瓜种植和销售.已知西瓜的成本为6元/千克,规定销售单价不低于成本,又不高于成本的两倍.经过市场调查发现,某天西瓜的销售量y(千克)与销售单价x(元/千克)的函数关系如下图所示:
(1)求y与x的函数解析式(也称关系式);
(2)求这一天销售西瓜获得的利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C,
(1)求这个二次函数的关系解析式;
(2)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出10件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出1件,若商场平均每天要盈利600元,每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为1,E为BC边的延长线上一点,CE=1,连接AE,与CD交于点F,连接BF并延长与线段DE交于点G,则BG的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰![]() 中,
中,![]() ,作
,作![]() 的外接圆⊙O.
的外接圆⊙O.
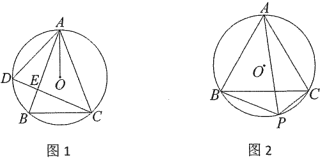
(1)如图1,点![]() 为
为![]() 上一点(不与A、B重合),连接AD、CD、AO,记
上一点(不与A、B重合),连接AD、CD、AO,记![]() 与
与![]() 的交点为
的交点为![]() .
.
①设![]() ,若
,若![]() ,请用含
,请用含![]() 与
与![]() 的式子表示
的式子表示![]() ;
;
②当![]() 时,若
时,若![]() ,求
,求![]() 的长;
的长;
(2)如图2,点![]() 为
为![]() 上一点(不与B、C重合),当BC=AB,AP=8时,设
上一点(不与B、C重合),当BC=AB,AP=8时,设![]() ,求
,求![]() 为何值时,
为何值时,![]() 有最大值?并请直接写出此时⊙O的半径.
有最大值?并请直接写出此时⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com