
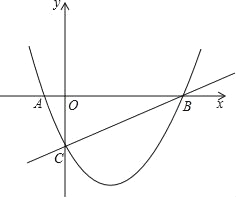
【题目】如图,已知抛物线y=ax2﹣![]() x+c与x轴相交于A、B两点,并与直线y=
x+c与x轴相交于A、B两点,并与直线y=![]() x﹣2交于B、C两点,其中点C是直线y=
x﹣2交于B、C两点,其中点C是直线y=![]() x﹣2与y轴的交点,连接AC.
x﹣2与y轴的交点,连接AC.
(1)求抛物线的解析式;
(2)证明:△ABC为直角三角形;
(3)△ABC内部能否截出面积最大的矩形DEFG?(顶点D、E、F、G在△ABC各边上)若能,求出最大面积;若不能,请说明理由.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2;(2)见解析;(3)△ABC内部可截出面积最大的矩形DEFG,面积为
x﹣2;(2)见解析;(3)△ABC内部可截出面积最大的矩形DEFG,面积为![]() .
.
【解析】分析:![]() 求出点
求出点![]() 的坐标,用待定系数法求二次函数解析式即可.
的坐标,用待定系数法求二次函数解析式即可.
![]() 分别求出
分别求出![]() 的长度,用勾股定理逆定理判定即可.
的长度,用勾股定理逆定理判定即可.
![]() 在直角三角形中截出矩形,面积最大,我们易得两种情形,①一点为C,AB、AC、BC边上各有一点,②AB边上有两点,AC、BC边上各有一点.讨论时可设矩形一边长x,利用三角形相似等性质表示另一边,进而描述面积函数.利用二次函数最值性质可求得最大面积.
在直角三角形中截出矩形,面积最大,我们易得两种情形,①一点为C,AB、AC、BC边上各有一点,②AB边上有两点,AC、BC边上各有一点.讨论时可设矩形一边长x,利用三角形相似等性质表示另一边,进而描述面积函数.利用二次函数最值性质可求得最大面积.
详解:(1)∵直线![]() 交x轴、y轴于B.C两点,
交x轴、y轴于B.C两点,
∴B(4,0),C(0,2),
∵![]() 过B.C两点,
过B.C两点,
∴![]() ,
,
解得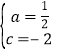 ,
,
∴![]()
(2)证明:如图1,连接AC,
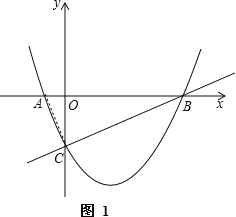
∵![]() 与x负半轴交于A点,
与x负半轴交于A点,
∴A(1,0),
在Rt△AOC中,
∵AO=1,OC=2,
∴![]()
在Rt△BOC中,
∵BO=4,OC=2,
∴![]()
∵AB=AO+BO=1+4=5,
∴![]()
∴△ABC为直角三角形.
(3)△ABC内部可截出面积最大的矩形DEFG,面积为![]() ,理由如下:
,理由如下:
①一点为C,AB、AC、BC边上各有一点,如图2,此时△AGF∽△ACB∽△FEB.
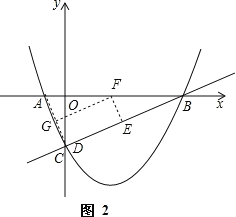
设![]()
∵![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
![]()
即当![]() 时,S最大,为
时,S最大,为![]()
②AB边上有两点,AC、BC边上各有一点,如图3,此时△CDE∽△CAB∽△GAD,
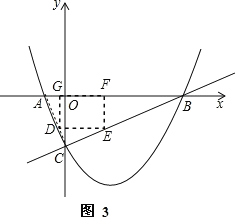
设GD=x,
∵![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
即x=1时,S最大,为![]()
综上所述,△ABC内部可截出面积最大的矩形DEFG,面积为![]()


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】我们知道,正整数的和1+3+5+…+(2n﹣1)=n2,若把所有正偶数从小到大排列,并按如下规律分组:(2),(4,6,8),(10,12,14,16,18),(20,22,24,26,28,30,32),…,现有等式Am=(i,j)表示正偶数m是第i组第j个数(从左到右数),如A8=(2,3),则A2018=_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过点B(0,2)的直线y=kx+b与x轴交于点C,与正比例函数y=ax的图象交于点A(﹣1,3)
(1)求直线AB的函数的表达式;
(2)直接写出不等式(kx+b)﹣ax<0的解集;
(3)求△AOC的面积;
(4)点P是直线AB上的一点,且知△OCP是等腰三角形,写出所有符合条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将1,2,3,...,30,这30个整数,任意分为15组,每组2个数.现将每组数中的一个数记为![]() ,另一个数记为
,另一个数记为![]() ,计算代数式
,计算代数式![]() 的值,15组数代入后可得到15个值,则这15个值之和的最小值为( )
的值,15组数代入后可得到15个值,则这15个值之和的最小值为( )
A.![]() B.120C.225D.240
B.120C.225D.240
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励居民节约用电,国家发改委发布文件在全国实行“阶梯电价”收费,重庆结合本市实际,根据国家发改委文件要求,决定从2016年1月1日起对居民生活用电实行“阶梯电价”收费,具体收费标准见下表.若2016年8月份,该市居民甲生活用电240千瓦时(能量量度单位,1千瓦时即1度),交电费130元.
一户居民一个月用电量 | 电费价格(元/千瓦时) | |
第一档 | 不超过200千瓦时 | 0.52 |
第二档 | 超过200千瓦时但不超过320千瓦时 |
|
第三档 | 超过320千瓦时 | 0.95 |
(1)求上表中的![]() 的值;
的值;
(2)若该市居民乙某月交电费220元,居民乙当月的生活用电量为多少千瓦时?
(3)实行“阶梯电价”收费后,该市居民丙月用电量为多少千瓦时,其当月的平均电价为0.55元/千瓦时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“母亲节”前夕,我市某校学生积极参与“关爱贫困母亲”的活动,他们购进一批单价为20元的“孝文化衫”在课余时间进行义卖,要求每件销售价格不得高于27元,并将所得利润捐给贫困母亲。经试验发现,若每件按22元的价格销售时,每天能卖出42件;若每件按25元的价格销售时,每天能卖出33件.假定每天销售件数y(件)与销售价格x(元/件)满足一个以x为自变量的一次函数.
(1)求y与x满足的函数关系式(不要求写出x的取值范围);
(2)在不积压且不考虑其他因素的情况下,销售价格定为多少元时,才能使每天获得的利润![]() 最大,最大利润是多少?
最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)从A地到B地,某甲走直径AB上方的半圆途径;乙先走直径AC上方半圆的途径,再走直径CB下方半圆的途径,如图1,已知AB=40米,AC=30米,计算个人所走的路程,并比较两人所走路程的远近;
(2)如果甲.乙走的路程图改成图2,两人走的路程远近相同吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,DE⊥BC交AC于点E,已知AD=AB,连接BE交AD于点F,下列结论:①BE=CE;②∠CAD=∠ABE;③S△ABF=3S△DEF;④△DEF∽△DAE,其中正确的有( )

A. 1个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com